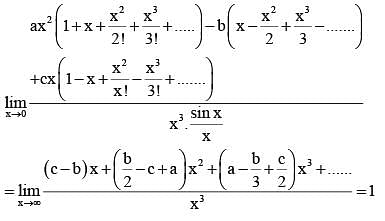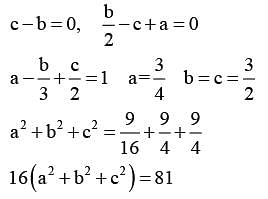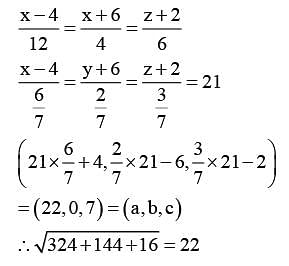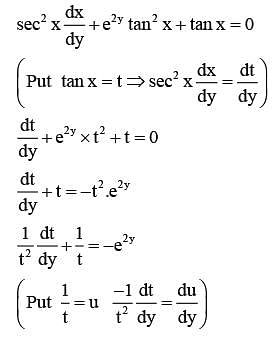Test: JEE Main 2024 January 31 Shift 2 - JEE MCQ
30 Questions MCQ Test JEE Main & Advanced Previous Year Papers - Test: JEE Main 2024 January 31 Shift 2
Let A (a, b), B (3, 4) and (−6,−8) respectively denote the centroid, circumcentre and orthocentre of a triangle. Then, the distance of the point P(2a + 3,7b + 5) from the line 2x + 3y − 4 = 0 measured parallel to the line x − 2y − 1 = 0 is
Let z1 and z2 be two complex numbers such that z1 + z2 = 5 and 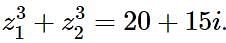 . Then
. Then  equals-
equals-
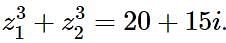 . Then
. Then  equals-
equals-| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let a variable line passing through the centre of the circle x2 + y2 - 16x - 4y = 0, meet the positive co-ordinate axes at the point A and B. Then the minimum value of OA + OB, where O is the origin, is equal to
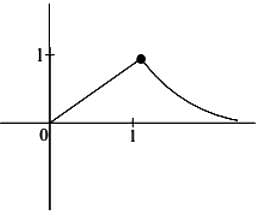
Let f, g: (0, ∞) → R be two functions defined by 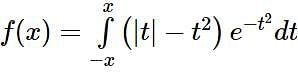 and
and 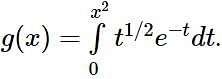 Then the value of
Then the value of 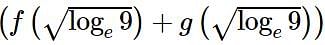 is equal to
is equal to
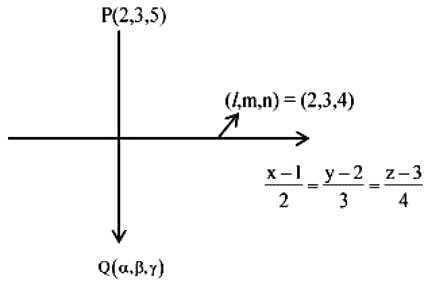
Let (α, β, γ) be mirror image of the point (2, 3, 5) in the line 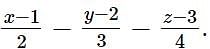 Then 2α + 3β + 4γ is equal to
Then 2α + 3β + 4γ is equal to
Let P be a parabola with vertex (2, 3) and directrix  . Let an ellipse
. Let an ellipse  of eccentricity
of eccentricity  pass through the focus of the parabola P. Then the square of the length of the latus rectum of E, is
pass through the focus of the parabola P. Then the square of the length of the latus rectum of E, is
The temperature T(t) of a body at time t = 0 is 160o F and it decreases continuously as per the
differential equation 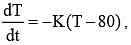 where K is positive constant. If T(15) = 120oF, then T(45) is equal to
where K is positive constant. If T(15) = 120oF, then T(45) is equal to
If 2nd, 8th, 44th terms of A.P. are 1st, 2nd and 3rd terms respectively of G.P. and first term of A.P. is 1 then the sum of first 20 terms of A.P. is
Let f: → R → (0, ∞) be a strictly increasing function such that 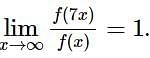 Then, the value of
Then, the value of 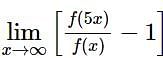 is equal to
is equal to
The area of the region enclosed by the parabola 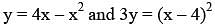 is equal to
is equal to
Let the mean and the variance of 6 observation a, b, 68, 44, 48, 60 be 55 and 194, respectively if a > b, then a + 3b is
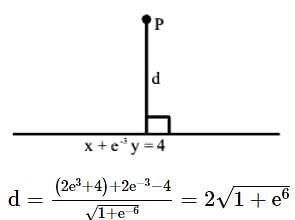
If the function f : (-∞, -1) → (a,b) defined by 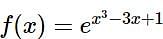 is one-one and onto, then the distance of the point P(2b + 4,a + 2) from the line x + e-3 y = 4 is
is one-one and onto, then the distance of the point P(2b + 4,a + 2) from the line x + e-3 y = 4 is
Consider the function f : (0, ∞) → defined by 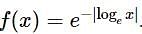 If m and n be respectively the number of points at which f is not continuous and f is not differentiable, then m+n is
If m and n be respectively the number of points at which f is not continuous and f is not differentiable, then m+n is
The number of solutions, of the equation esin x - 2e -sin x = 2 is
A coin is based so that a head is twice as likely to occur as a tail. If the coin is tossed 3 times, then the probability of getting two tails and one head is-
The shortest distance between lines L1 and L2, where 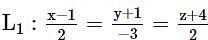 and L2 is the line passing through the points A(-4,4,3).B(-1,6,3) and perpendicular to the line
and L2 is the line passing through the points A(-4,4,3).B(-1,6,3) and perpendicular to the line 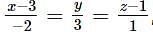 is
is
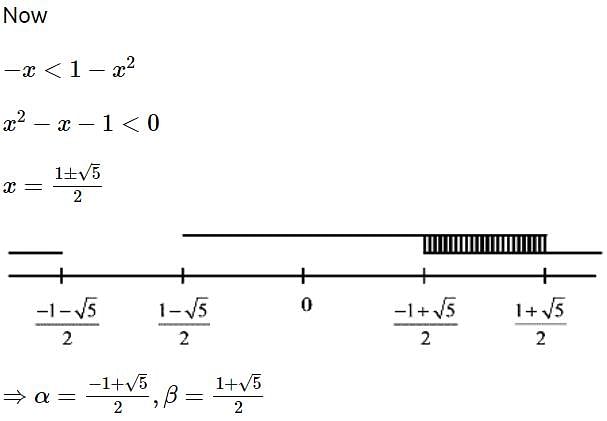
Let a, b, c be the length of three sides of a triangle satisfying the condition (a2 +b2) x2 - 2b (a + c)x + (b2 + c2) = 0. If the set of all possible values of x is the interval (α, β), then 12 (α2 + β2) is equal to
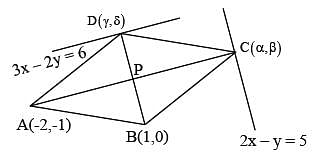
Let A(–2, –1), B(1, 0), C(α,β) and 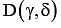 be the vertices of a parallelogram ABCD . If the point C lies on
be the vertices of a parallelogram ABCD . If the point C lies on 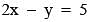 and the point D lies on
and the point D lies on  , then the value of
, then the value of 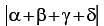
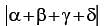 is equal to _______ .
is equal to _______ .
Let the coefficient of xr in the expansion of

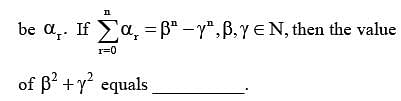
Let A be a 3 x3 matrix and det (A) = 2. If
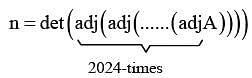
Then the remainder when n is divided by 9 is equal to ___________.
Let 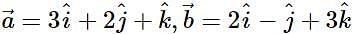 and
and 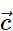 be a vector such that
be a vector such that 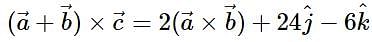 and
and 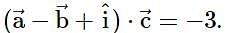 . Then
. Then 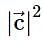 is equal to _____.
is equal to _____.
A line passes through A(4, –6, –2) and B(16, –2,4). The point P(a, b, c) where a, b, c are non-negative integers, on the line AB lies at a distance of 21 units, from the point A. The distance between the points P(a, b, c) and Q(4, –12, 3) is equal to ____.
Let y = y(x) be the solution of the differential equation
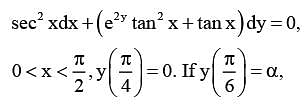
Then e8α is equal to ______.
Let A = {1, 2, 3, ………100}. Let R be a relation on A defined by (x, y) ∈R if and only if 2x = 3y. Let R1 be a symmetric relation on A such that  and the number of elements in R1 is n. Then, the minimum value of n is ___________.
and the number of elements in R1 is n. Then, the minimum value of n is ___________.
A light string passing over a smooth light fixed pulley connects two blocks of masses and . If the acceleration of the system is , then the ratio of masses is

|
254 docs|1 tests
|
|
254 docs|1 tests
|


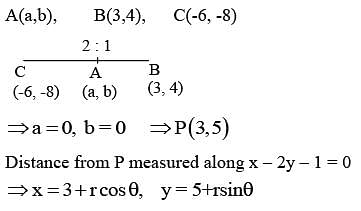
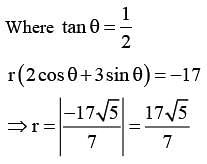
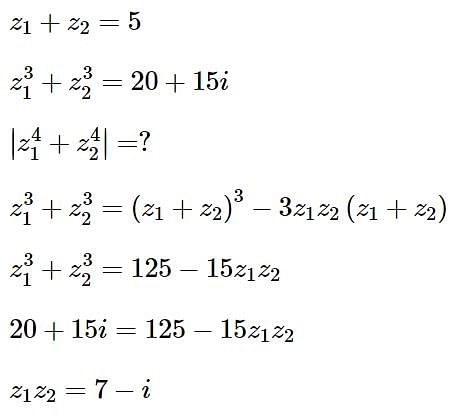

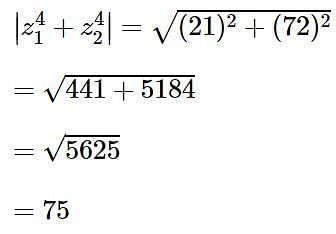

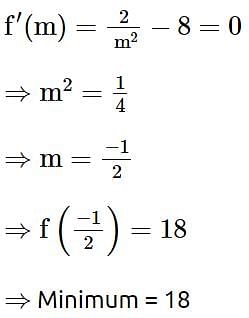
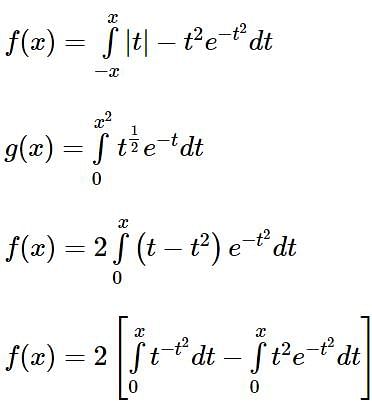
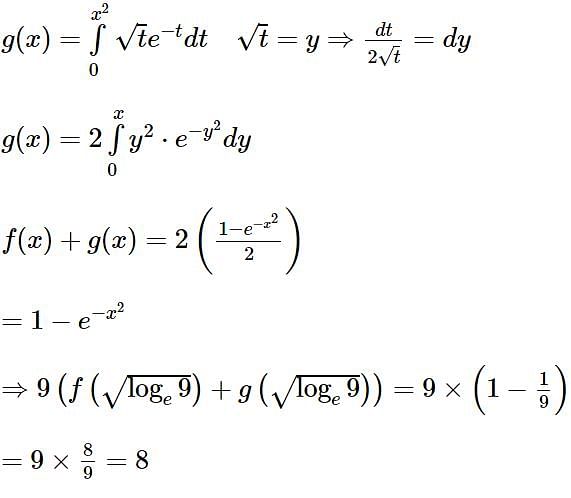
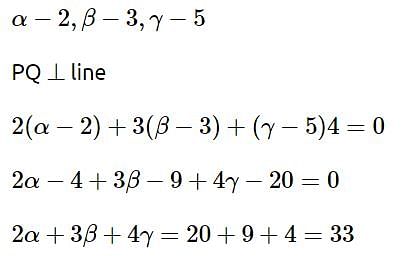








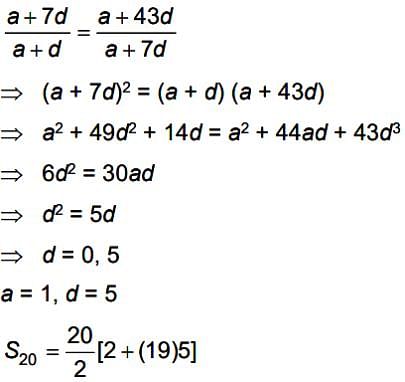
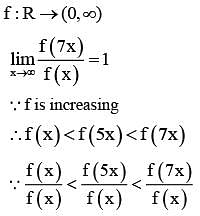
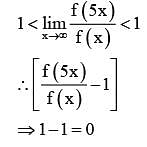

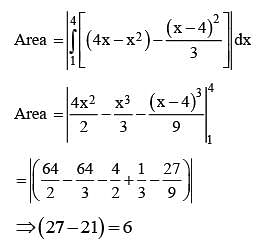

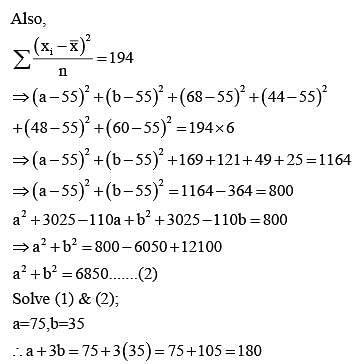
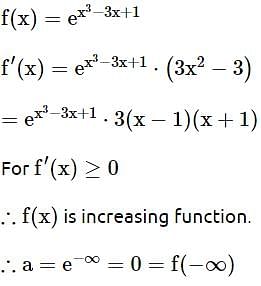
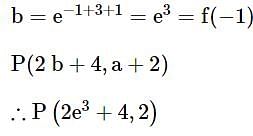
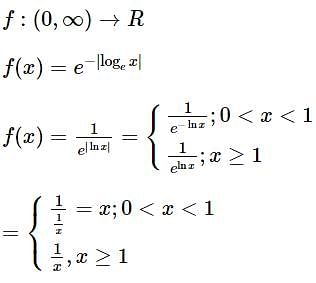
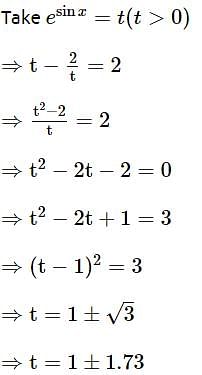
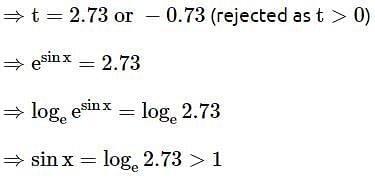
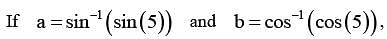 , then
, then  is equal to
is equal to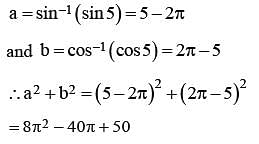
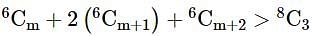 and
and 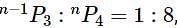 , then
, then 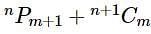 is equal to
is equal to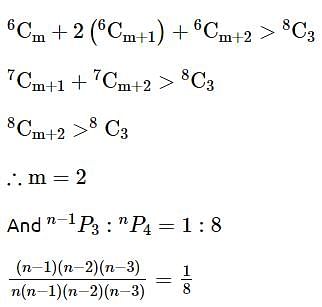
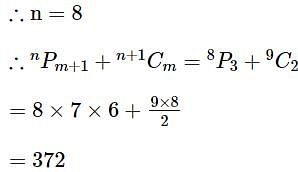
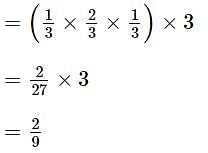
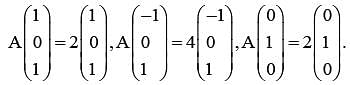

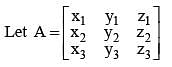
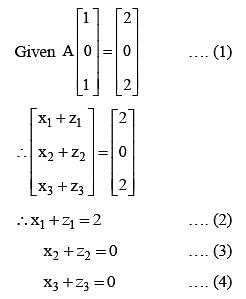


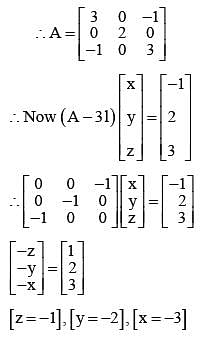
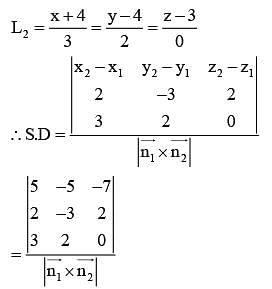
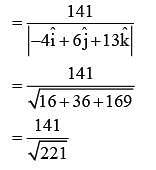
 is equal to .
is equal to . 
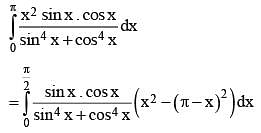

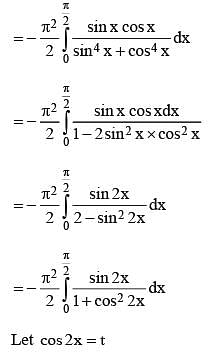

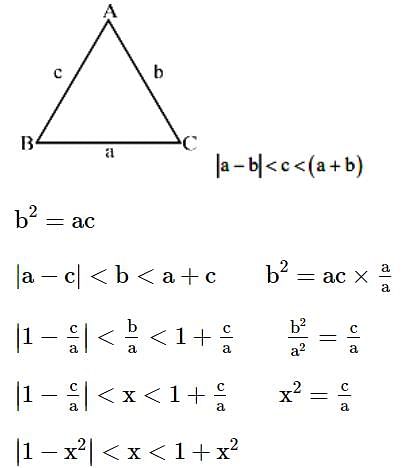
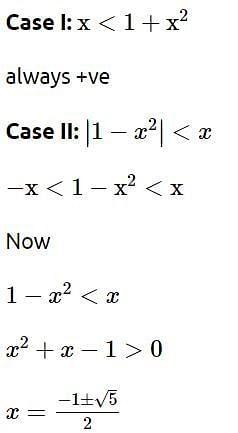
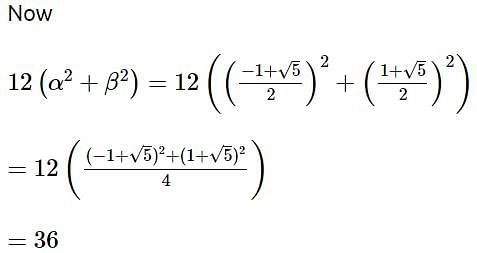
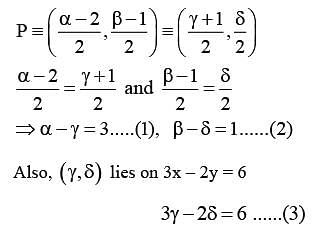
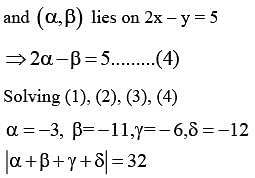
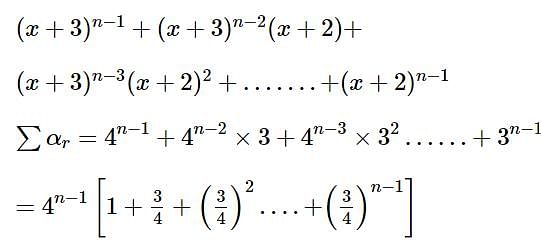
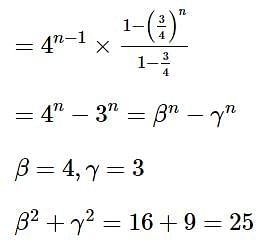
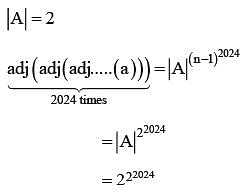
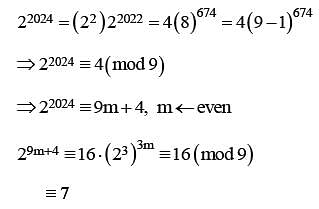
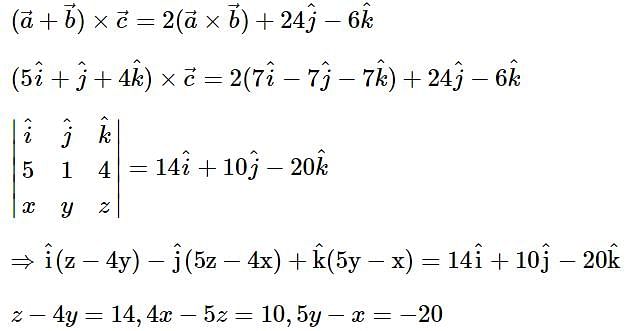
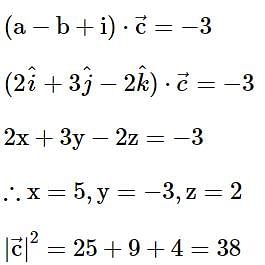
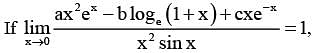 then 16(a2 + b2 + c2) is equal to ______.
then 16(a2 + b2 + c2) is equal to ______.