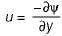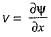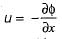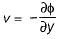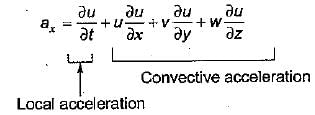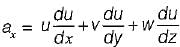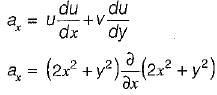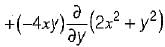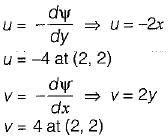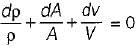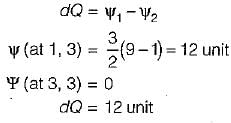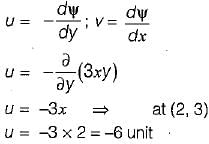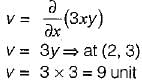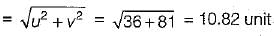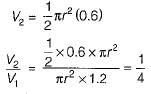Test: Kinematics of Flow & Ideal Flow - 3 - Mechanical Engineering MCQ
15 Questions MCQ Test - Test: Kinematics of Flow & Ideal Flow - 3
In a two-dimensional flow, the velocity components in x and y directions in terms of stream function (ψ) are
If φ is the velocity potential function in 2-D flow field, then the velocity components u and v are defined as
The convective acceleration of fluid in the x-direction is given by
A steady incompressible flow is given by
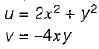
Q. What is the convective acceleration along x-direction at point (1, 2)?
Match List-I with List-ll and select the correct answer using the codes given below the lists:
List-I
A. Stream line
B. Streak line
C. Path line
D. Equipotential lines
List-II
1. Tracing of motion of any fluid particle
2. Tracing of motion of different fluid particles
3. Identification of location of number of fluid particles
4. Orthogonal to streak lines
5. Location of equal piezometric head
Codes:
A B C D
(a) 2 3 4 5
(b) 3 2 1 4
(c) 1 2 4 3
(d) 2 3 1 5
The stream function for a two-dimensional flow is given by ψ = 2xy. The velocity at (2, 2) is
You are asked to evaluate assorted fluid flows for their suitability in a given laboratory application. The following three flow choices, expressed in terms of 2-D velocity field in the xy plane, are made available
P. u = 2y,v = -3x
Q. u = 3xy, v = 0
R. u = -2x , v = 2 y
Which flow(s) should be recommended when the application requires the flow to be incompressible and irrotational
The continuity equation in differential form is
Given φ = 3 xy and ψ = 3/2(y2 - x2) , the discharge passing between the stream tines through the point (1,3) and (3,3) is
If the stream function is given by ψ = 3xy then the velocity at a point (2,3) will be
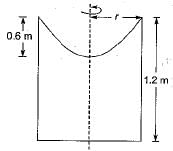
An open circular cylinder 1.2 m height is filled with a liquid to its top. The liquid is given a rigid body rotation about the axis of the cylinder and the pressure at the centre line at the bottom surface is found to be 0.6 m of liquid. What is the ratio of volume of liquid spilled out of the cylinder to the original volume
In a two dimensional velocity field with velocities u and v along the x and y directions respectively the convective acceleration along the x-direction is given by
A type of flow in which the fluid particle while moving in the direction of flow rotates about their centre is known as
For the continuity equation given by 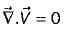 to be valid, where
to be valid, where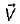 is the velocity vector, which one of the following is a necessary condition?
is the velocity vector, which one of the following is a necessary condition?