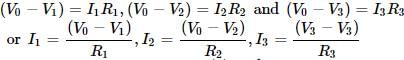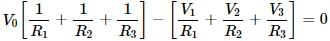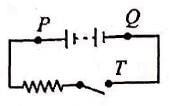Test: Kirchhoff's Laws (NCERT) - NEET MCQ
10 Questions MCQ Test NCERTs at Fingertips: Textbooks, Tests & Solutions - Test: Kirchhoff's Laws (NCERT)
Point out the right statements about the validity of Kirchhoff's junction rule
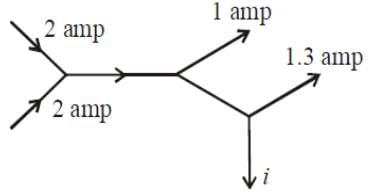
The figure below shows currents in a part of electric circuit. The current i is

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
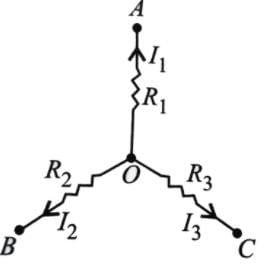
A circuit has a section ABC if the potential at point A, B and C are V1, V2 and V3 respectively, calculate the potential at point O is
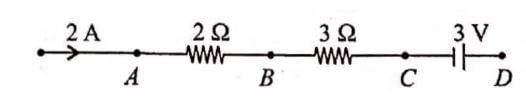
The potential difference between A and B in figure is
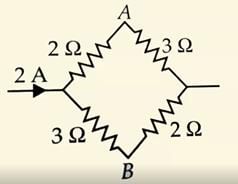
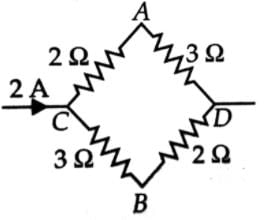
In the given circuit the potential at point B is zero, the potential at points A and D will be
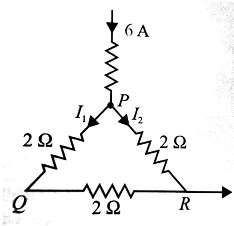
A current of 6A enters one corner P of an equilateral triangle PQR having 3 wires of resistances 2 Ω each and leaves by the corner R. Then the current I1 and I2 are
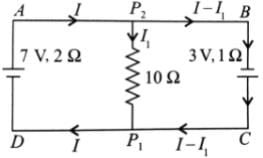
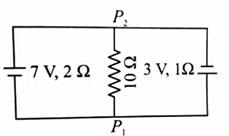
A 7V battery with internal resistance 3Ω and 3V battery with internal resistance 10mega are connected to a 10Ω resistors as shown in figure, the current in 10Ω resistor is
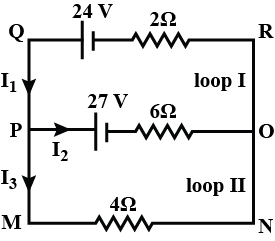
In the circuit shown, the value of currents I1, I2 and I3 are
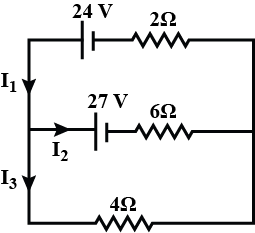
In the circuit shown, current flowing through 25V cell is
A battery, an open switch and a resistor are connected in series as shown in figure.
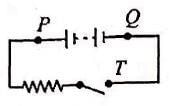
Consider the following three statements concerning the circuit. A voltmeter will read zero if it is connected across points
(i) P and T
(ii) P and Q
(iii) Q and T
Which one of the above is/are true?
|
257 docs|234 tests
|
|
257 docs|234 tests
|