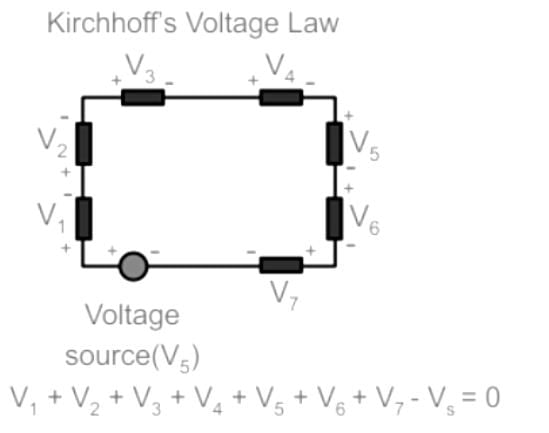
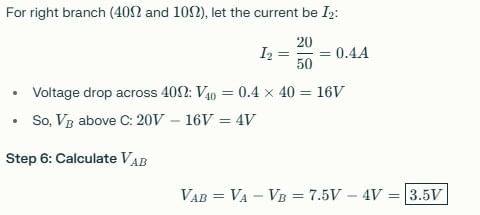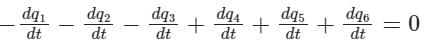Electrical Engineering (EE) Exam > Electrical Engineering (EE) Tests > Test: Kirchhoff’s Current & Voltage Law - Electrical Engineering (EE) MCQ
Test: Kirchhoff’s Current & Voltage Law - Electrical Engineering (EE) MCQ
Test Description
20 Questions MCQ Test - Test: Kirchhoff’s Current & Voltage Law
Test: Kirchhoff’s Current & Voltage Law for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Test: Kirchhoff’s Current & Voltage Law questions and answers have been prepared
according to the Electrical Engineering (EE) exam syllabus.The Test: Kirchhoff’s Current & Voltage Law MCQs are made for Electrical Engineering (EE) 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Kirchhoff’s Current & Voltage Law below.
Solutions of Test: Kirchhoff’s Current & Voltage Law questions in English are available as part of our course for Electrical Engineering (EE) & Test: Kirchhoff’s Current & Voltage Law solutions in
Hindi for Electrical Engineering (EE) course.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free. Attempt Test: Kirchhoff’s Current & Voltage Law | 20 questions in 20 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study for Electrical Engineering (EE) Exam | Download free PDF with solutions
Test: Kirchhoff’s Current & Voltage Law - Question 1
Find the value of v if v1 = 20V and value of current source is 6A
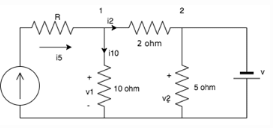
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 1
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 2
Test: Kirchhoff’s Current & Voltage Law - Question 3
Calculate the current across the 20 ohm resistor.
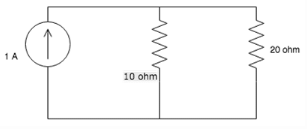
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 3
Test: Kirchhoff’s Current & Voltage Law - Question 4
Calculate the value of I3, if I1 = 2A and I2 = 3A
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 4
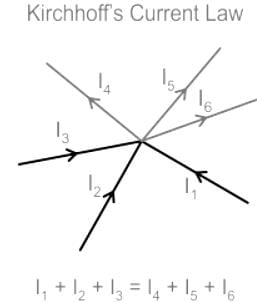
Test: Kirchhoff’s Current & Voltage Law - Question 5
Find the value of i2, i4 and i5 if i1 = 3A, i3 = 1A and i6 = 1A
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 5
Test: Kirchhoff’s Current & Voltage Law - Question 6
What is the value of current if a 50C charge flows in a conductor over a period of 5 seconds?
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 6
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 7
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 8
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 9
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 10
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 11
Test: Kirchhoff’s Current & Voltage Law - Question 12
Calculate the voltage across the 10 ohm resistor.
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 12
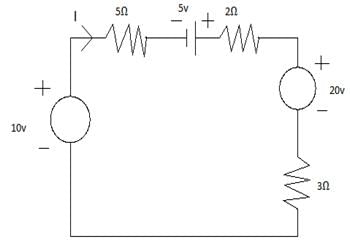
Test: Kirchhoff’s Current & Voltage Law - Question 13
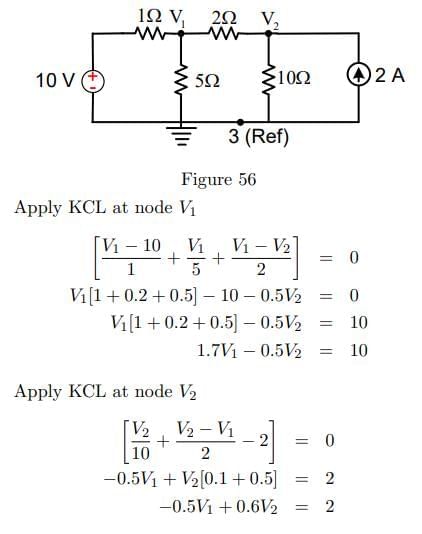
In the circuit shown in Figure determine voltage at the node connecting 1 ohm, 2 ohm and 5 ohm resistor
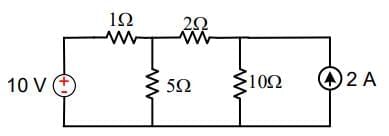
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 13
Test: Kirchhoff’s Current & Voltage Law - Question 14
The sum of the voltages over any closed loop is equal to __________
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 14
Test: Kirchhoff’s Current & Voltage Law - Question 15
What is the basic law that has to be followed in order to analyze any circuit?
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 15
Test: Kirchhoff’s Current & Voltage Law - Question 16
Every____________ is a ____________ but every __________ is not a __________
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 16
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 17
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 18
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 19
Test: Kirchhoff’s Current & Voltage Law - Question 20
Which of the following facts is correct for KCL?
Detailed Solution for Test: Kirchhoff’s Current & Voltage Law - Question 20
Information about Test: Kirchhoff’s Current & Voltage Law Page
In this test you can find the Exam questions for Test: Kirchhoff’s Current & Voltage Law solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Kirchhoff’s Current & Voltage Law, EduRev gives you an ample number of Online tests for practice
Download as PDF