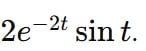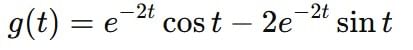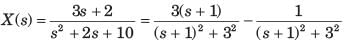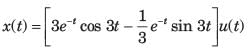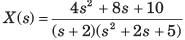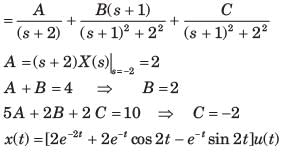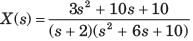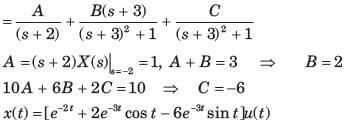Test: Laplace Transform- 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Laplace Transform- 2
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 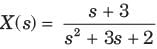
Q.
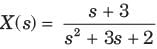
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 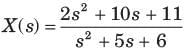
Q.
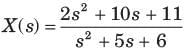
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 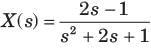
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 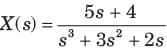
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 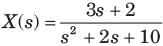
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 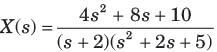
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 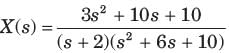
The Laplace transform of the differential equation y" + ay' + by = f(t). Assume that y(0) = 5, y'(0) = 10, Y(s) and F(s) are the Laplace transforms of y(t) and f(t) respectively


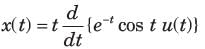
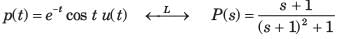
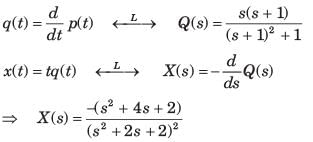

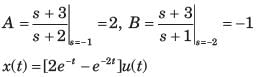

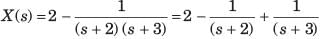
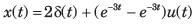
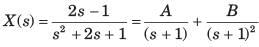
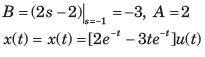
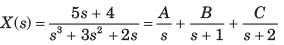
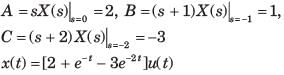
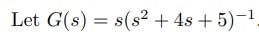 the inverse transform of G(s) is
the inverse transform of G(s) is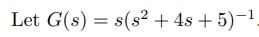
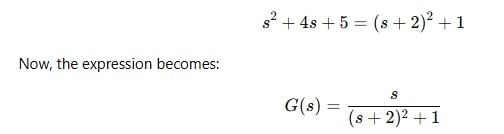
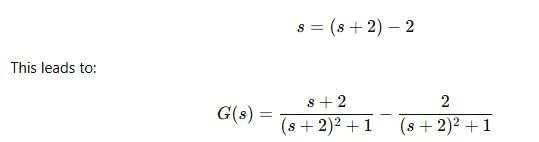
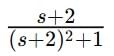 corresponds to the inverse Laplace transform of
corresponds to the inverse Laplace transform of 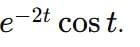
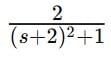 corresponds to the inverse Laplace transform of
corresponds to the inverse Laplace transform of