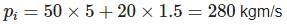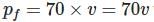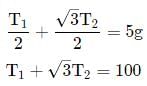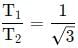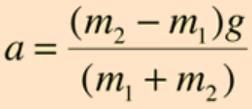Test: Laws of Motion - 3 - JEE MCQ
30 Questions MCQ Test - Test: Laws of Motion - 3
You are on a friction less horizontal plane. How can you get off if no horizontal force is exerted by pushing against the surface ?
The forces acting on an object are shown in the fig. If the body moves horizontally at a constant speed of 5 m/s, then the values of the forces P and S are, respectively-


A boy of mass 50 Kg running at 5 m/s jumps on to a 20Kg trolley travelling in the same direction at 1.5 m/s. What is the common velocity?
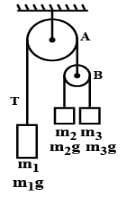
Find the velocity of the hanging block if the velocities of the free ends of the rope are as indicated in the figure.
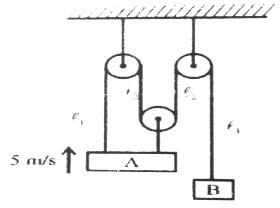
At a given instant, A is moving with velocity of 5 m/s upwards. What is velocity of B at the time

A body of mass 5 kg is suspended by the strings making angles 60º and 30º with the horizontal -
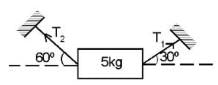
(a) T1 = 25 N
(b) T2 = 25 N
(c) T1 = 25N
(d) T2 = 25N
A cyclist of mass 30 kg exerts a force of 250 N to move his cycle. acceleration is 4 ms−2. force of friction between road and tyres will be
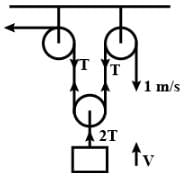
In the arrangement shown in fig. the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed. Mass M moves upwards with a speed.
The velocity of end `A' of rigid rod placed between two smooth vertical walls moves with velocity `u' along vertical direction. Find out the velocity of end `B' of that rod, rod always remains in constant with the vertical walls.
A cyclist of mass 30 kg exerts a force of 250 N to move his cycle. The acceleration is 4 ms−2. The force of friction between the road and tyres will be
Find out the reading of the weighing machine in the following cases.
A mass M is suspended by a rope from a rigid support at A as shown in figure. Another rope is tied at the end B, and it is pulled horizontally with a force F. If the rope AB makes an angle q with the vertical in equilibrium, then the tension in the string AB is :
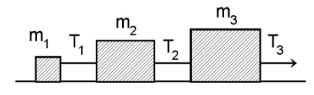
Three block are connected as shown, on a horizontal frictionless table and pulled to the right with a force T3 = 60 N. If m1 = 10 kg, m2 = 20 kg and m3 = 30 kg, the tension T2 is-
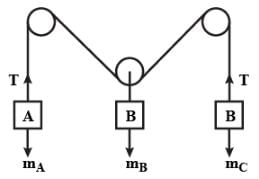
Three blocks A, B and C are suspended as shown in the figure. Mass of each blocks A and C is m. If system is in equilibrium and mass of B is M, then :
A weight can be hung in any of the following four ways by string of same type. In which case is the string most likely to break ?
A force-time graph for a linear motion is shown in figure where the segments are circular. The linear momentum gained between zero and 8 seconds in -
A particle moves in the xy plane under the action of a force F such that the value of its linear momentum (P) at any time t is, Px = 2 cost, Py = 2 sint. The angle q between P and F at that time t will be -
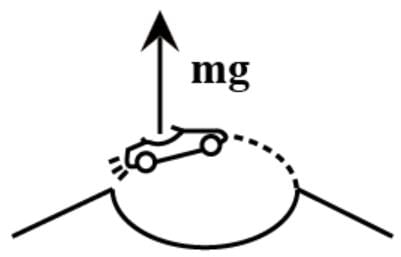
A stunt man jumps his car over a crater as shown (neglect air resistance)
A particle of mass 50 gram moves on a straight line. The variation of speed with time is shown in figure. find the force acting on the particle at t = 2, 4 and 6 seconds.
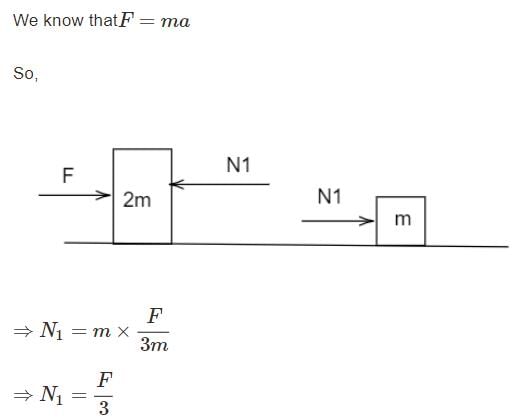
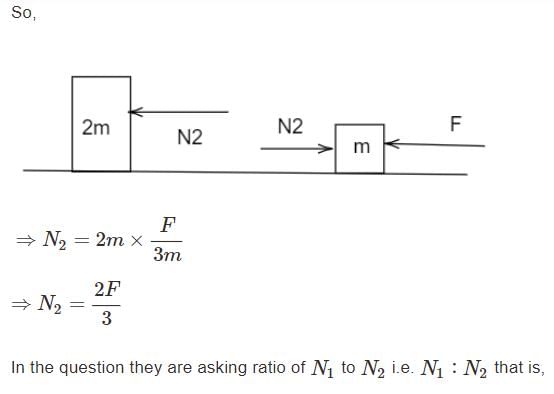
Two blocks are in contact on a frictionless table. One has mass m and the other 2m. A force F is applied on 2m as shown in the figure. Now the same force F is applied from the right on m. In the two cases respectively, the ratio force of contact between the two block will be :
A body of mass 8 kg is hanging another body of mass 12 kg. The combination is being pulled by a string with an acceleration of 2.2 m s-2. The tension T1 and T2 will be respectively : (use g = 9.8 m/s2)
A rope of mass 5 kg is moving vertically in vertical position with an upwards force of 100 N acting at the upper end and a downwards force of 70 N acting at the lower end. The tension at midpoint of the rope is
A particle of small mass m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force in the pulley is
The pulley arrangements shown in figure are identical the mass of the rope being negligible. In case I, the mass m is lifted by attaching a mass 2 m to the other end of the rope. In case II, the mass m is lifted by pulling the other end of the rope with cosntant downward force F = 2 mg, where g is acceleration due to gravity. The acceleration of mass in case I is
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination a and b. The tension in the string is:
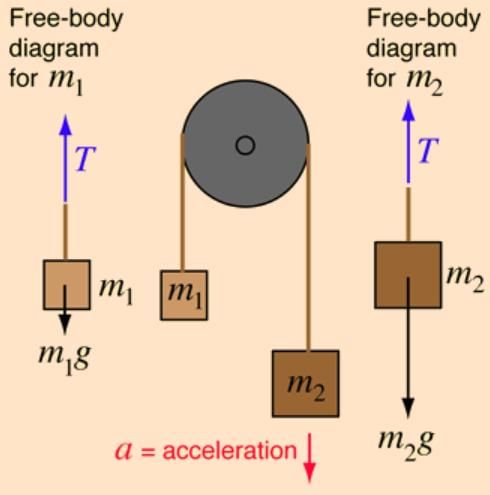
Two masses are hanging vertically over frictionless pulley. The acceleration of the two masses is-
Three equal weights A, B, C of mass 2 kg each are hanging on a string passing over a fixed frictionless pulley as shown in the fig. The tension in the string connecting weights B and C is-
In the arrangement shown in figure, pulleys are massless and frictionless and threads are inextensible. The Block of mass m1 will remain at rest, if
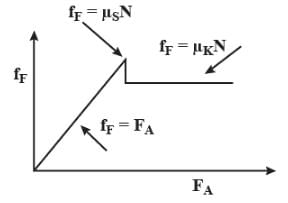
A block is placed on a rough floor and a horizontal force F is applied on it. The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them-