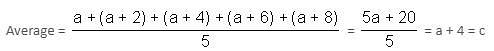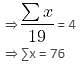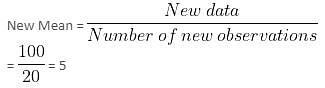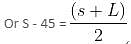Test Level 1: Averages - 1 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 1: Averages - 1
Find the average of five consecutive even numbers a, b, c, d and e.
At present, the average age of a father and his son is 29 years. The average age of father, mother and son five years from now will be 37 years. Find the mother's present age.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A student scores an average of 80 marks in six subjects. If the subjects with the highest and the lowest scores are excluded, the average decreases by 1. If his highest score in a subject is 86, what is his lowest score?
The mean of 19 observations is 4. If one more observation of 24 is added to the data, the new mean will be
The average monthly salary of employees, consisting of officers and workers, of an organisation is Rs. 3000. The average salary of an officer is Rs. 10,000, while that of a worker is Rs. 2000 per month. If there are total 400 employees in the organisation, find the number of officers.
The average of ten numbers is 27. If the smallest number is deleted from the list, the average of the remaining 9 numbers will be x and if the largest number is deleted, the average will be y. What is the average of the smallest and the largest numbers, if x + y = 10?
How many pairs of positive integers, not more than 100, will have an average greater than 50?
The average marks of a student in 10 papers are 80. If the highest and the lowest scores are not considered, the average is 81. If his highest score is 92, find the lowest.
Total expenses of a boarding house are partly fixed and partly varying linearly with the number of boarders. The average expense per boarder is Rs. 700 when there are 25 boarders and Rs. 600 when there are 50 boarders. What is the average expense per boarder when there are 100 boarders?
|
5 docs|272 tests
|