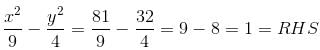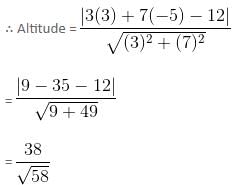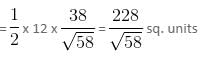Test Level 1: Coordinate Geometry - CAT MCQ
15 Questions MCQ Test - Test Level 1: Coordinate Geometry
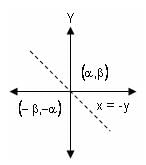
The image of the point (α, β) in the line x + y = 0 is
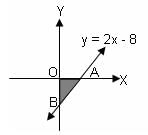
In the diagram, the line with equation y = 2x - 8 crosses x-axis at A and y-axis at B. The area of ΔAOB is

If x-form (x, y) = (x2 + x, y2 - y) and y-form (x, y) = (x2 - 11 , y2) are two functions defined on a plane, then find the distance between the points x-form (-2, 5) and y-form (5, -2)
Find the equation of the straight line passing through the point (-2, -3) and perpendicular to the line passing through (-2, 3) and (-5, -6).
The lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are perpendicular to each other if
Find the coordinates of the point which divides P1(1, -4) and P2(4, 2) externally in the ratio 1 : 4.
The vertices of a triangle are at (0, 0), (8, 0) and (0, 14). The orthocentre of the triangle is at
If A (a, 0) and B (3a, 0) are the vertices of an equilateral triangle ABC, then what are the coordinates of C?
The equation of the straight line which passes through the point (3, 4) and makes an intercept on the y-axis twice as long as that on the x-axis is
The value of k for which the circles x2 + y2 - 3x + ky - 5 = 0 and 4x2 + 4y2 - 12x - y - 9 = 0 become concentric is
What is the equation of a straight line which passes through the point of intersection of the straight lines x – 3y + 1 = 0 and 2x + 5y – 9 = 0 and has infinite slope?
A triangle has 12 units base on the line 3x + 7y = 12. If the third vertex is at point (3, - 5), find the area of the triangle.
The area of the circle x2 + y2 - 6x - 8y - 24 = 0 is
If u = a1x + b1y + c1 = 0, v = a2x + b2y + c2 and a1/a2 = b1/b2 = c1/c2 , then locus of the equation u + λv = 0, λ ∈ R is




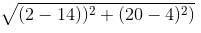
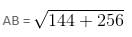
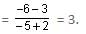

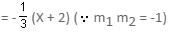
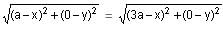
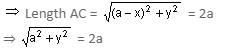
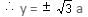
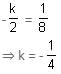
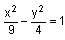 passes through the point
passes through the point