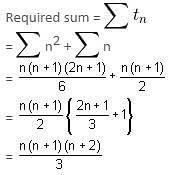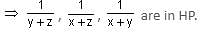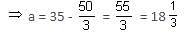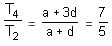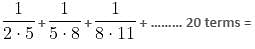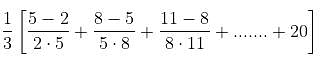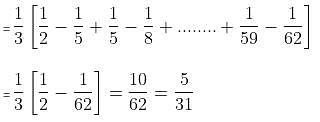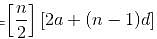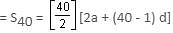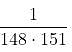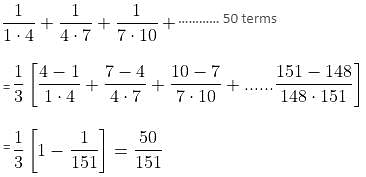Test Level 1: Progressions, Sequences & Series - 1 (August 5) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test Level 1: Progressions, Sequences & Series - 1 (August 5)
Find the value of 12 + 1 + 22 + 2 + 32 + 3 + ... + n2 + n.
If x, y, z are in AP, then 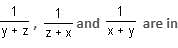
The ninth term of an AP is 5 more than the sixth term. If the eleventh term of that AP is 35, then what is its first term?
The sum of the 9th, 14th and 18th terms of an AP is equal to the sum of the 20th and 24th terms. What is the ratio of the 4th term to the 2nd term?
If a, b, c and d are in GP, then (a - c)2 + (b - c)2 + (b - d)2 is equal to
Susan had arranged to pay off her debt of $3,600 to CASA Bank in 40 monthly installments in the form of an A.P. When 30 of the installments had been repaid, she died leaving one third of the debt unpaid. What was the value of the first installment?
The sum of 5 numbers in AP is 75 and the product of the greatest and the least of them is 161. What is the greatest number?
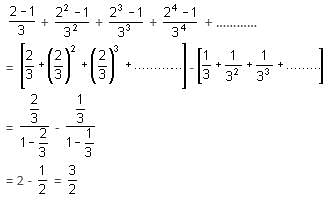
Find the sum of the infinite series: 1/3 + 3/9 + 7/27 + 15/81 + ............
Find the value of 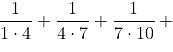 ..........… 50 terms.
..........… 50 terms.
|
152 docs|327 tests
|