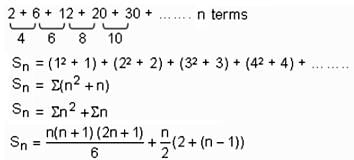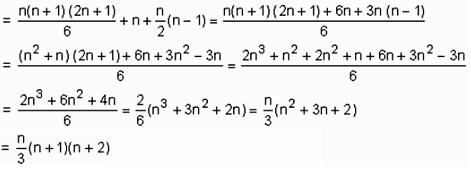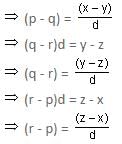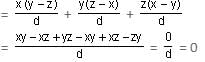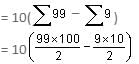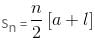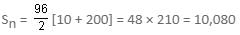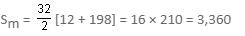Test Level 1: Progressions, Sequences & Series - 2 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 1: Progressions, Sequences & Series - 2
Four positive numbers are in geometric progression. Their sum is 156. The sum of the first and the third numbers is 1/5th of the sum of the second and the fourth numbers. Find the first number.
If a, b, c, d, e and f are AMs between 2 and 12, then a + b + c + d + e + f is equal to
2 + 6 + 12 + 20 + 30 + … up to n terms equals
The sum of 3rd and 15th terms of an arithmetic progression is equal to the sum of 6th, 11th and 13th terms of the same progression. Which term of the given progression should necessarily be equal to zero?
If the pth, qth, rth terms of an AP are x, y, z, respectively, then x(q - r) + y(r - p) + z(p - q) is equal to
What is the sum of all 3-digit numbers, which end with zero?
If the fifth term of an AP is twice its third term, then the first term of the AP is
If a, b, c are in AP and x, y, z are in GP, then xb - c. yc - a. za - b equals
The sum of 3rd and 15th terms of an arithmetic progression is equal to the sum of 6th, 11th and 13th terms of the same progression. Which term of the given progression should necessarily be equal to zero?
Find the sum of all even numbers from 10 to 200 (inclusive), excluding those, which are multiples of 6.
|
5 docs|250 tests
|