Test Level 1: Set Theory- 1 (May 14) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test Level 1: Set Theory- 1 (May 14)
In a group of 50 persons, everyone takes either tea or coffee. If 35 take tea and 25 take coffee, then the number of persons who take tea only (and not coffee) is
Let A = {x : x is a multiple of 3} and B = {x : x is a multiple of 5}. Then, A ∩ B is given by
Let A denote the set of integers between 1 and 1000 which are divisible by 12 and B denote the set of integers between 1 and 1000 which are divisible by 18. How many elements are there in the set A B?
Directions: Study the following information and answer the question.
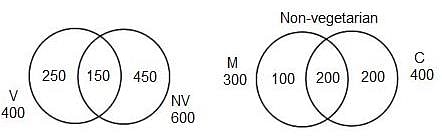
In Foodpur, where a person has to eat either vegetarian food or non-vegetarian food, there are 600 people who eat non-vegetarian food, 400 people who eat vegetarian food and 150 people who eat both. Of the people who eat non-vegetarian, there are 300 who eat mutton, 400 who eat chicken and 200 who eat both these types of meat.
Q. How many people eat non-vegetarian food, but do not eat mutton or chicken?
Directions: Study the following information and answer the question.
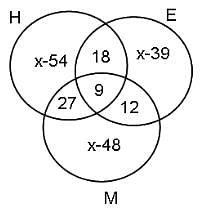
A newsagent sells the dailies Hindu, Express and Mail in equal number to 906 persons. 21 persons buy Express and Mail, 36 buy Hindu and Mail, 27 buy Hindu and Express, and buy 9 all the three dailies.
Q. The numbers of persons buying Hindu and Express only, Hindu and Mail only, and Express and Mail only form a ratio
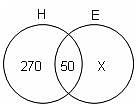
Members of a group of 400 people speak either Hindi or English or both. If 270 speak Hindi only and 50 speak both Hindi and English, then how many of them speak English only?
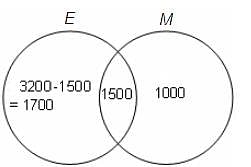
In a town with population of 5000, 3200 people are egg-eaters, 2500 meat eaters and 1500 eat both egg and meat. How many are pure vegetarians i.e. neither meat-eaters nor egg-eaters?
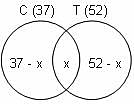
In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?
In a community, 56% of the total families use mixers and 66% of the total use air conditioners.
What is the highest number of families not using either a mixer or an air conditioner?
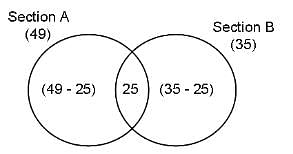
In a written test, out of number of students who appeared, 49% passed section A and 35% passed section B. Find the percentage of students who appeared but failed in both the sections of the test if 25% of the students passed both sections A and B.
|
152 docs|327 tests
|