Test Level 2: Clocks & Calendars - 2 - CAT MCQ
20 Questions MCQ Test Level-wise Tests for CAT - Test Level 2: Clocks & Calendars - 2
At what time between 5 and 6 o'clock will the hands of a clock be 3 minutes apart?
In the year 1648, if February had 5 Sundays, then what was the day on February 13, 1750?
At what time between 4 o'clock and 5 o'clock will the hands of a clock be at a right angle?
At what time between 4:15 a.m. and 5:05 a.m. will the angle between the hour hand and the minute hand of a clock be the same as the angle between the hands at 8:45 p.m.?
Alex turned a clock on at 3:00 pm. But the clock is defective, due to which it lags behind by 9 minutes after each day (24 hours). What will be the real time when the clock indicates 6:00 am on the 4th day of it's successive working?
If 15th March, 2013 was a Friday, then 10th July, 2013 will be a
At what time between 7 o'clock and 8 o'clock will the hands of a clock be in a straight line but not together?
How many days will there be from 23rd January, 2011 to 31st July, 2013 (both days included)?
Two clocks are set correctly at 10 a.m. on Friday. The first clock gains 2 minutes per hour, which is twice as much as gained by the second clock. What time will the second clock register when the correct time is 2 p.m. on the following Monday?
A man went outside between 7 o'clock and 9 o'clock at such a time that the minute hand and the hour hand were found to be coinciding before 8 o'clock; and when he returned, again he found both the hands to be coinciding, but after 8 o'clock. What was the time when he returned to the house?
A clock gains 2 minutes in an hour and an other clock loses 4 minutes in an hour. If both these clocks were set at 8 a.m, what will be the time in the first clock, if the second clock shows 10 p.m?
At what time between 9 and 10 will the hands of a clock be together?
What day of the week was it on 15th August, 1987?
How many times during a day will the hour hand and the minute hand of a clock be six minutes apart?
In a college, a 24-hour watch loses 5 minutes in 3 hours. If it is set correct on Tuesday midnight, then when will the watch show the correct time next?
A clock shows the time as 6 am. If the minute hand gains 2 minutes every hour, then how many minutes will the clock gain by 9 pm?
A tutor teaches 8 days consecutively and then takes off on the ninth day. If he starts teaching on Monday, then on what day of the week will he get his 12th off day?
I purchased some clocks from a second hand goods store. There were some problems in them. When the actual time passed 1 hour, the wall clock was 10 minutes behind it. When 1 hour was shown by the wall clock, the table clock showed 10 minutes ahead of it. When table clock showed 1 hour, the alarm clock was 5 minutes behind it. When alarm clock showed 1 hour, the wrist watch was 5 minutes ahead of it. Assuming that all clocks are correct with actual time at 12 noon, what will be shown by the wrist watch after 6 hours?
Today is Friday. A person wants to take a doctor's appointment. As the doctor is busy, he asks him to come three days after the day before the day after tomorrow. On which of the following days does the doctor ask the person to come?
If the current time is 6:20, then after how much time will the hands of the clock make the same angle as they do at present?
|
5 docs|250 tests
|


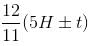
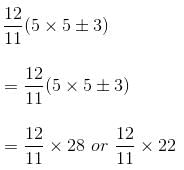
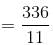 mins or 24 mins
mins or 24 mins
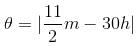 [where θ = angle between the hour-hand and the minute-hand, m - minutes, h - hours]
[where θ = angle between the hour-hand and the minute-hand, m - minutes, h - hours]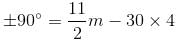
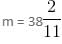 minutes past 4 or m =
minutes past 4 or m = 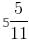 minutes past 4.
minutes past 4.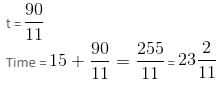
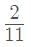 minutes past 4 o'clock
minutes past 4 o'clock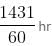 on this clock = 24 hr on the correct clock
on this clock = 24 hr on the correct clock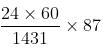 hr on the correct clock
hr on the correct clock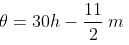
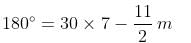
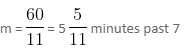
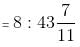
 = 90 minutes.
= 90 minutes.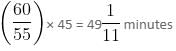
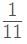 minutes past 9, the hands of the clock will be together.
minutes past 9, the hands of the clock will be together.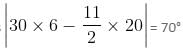
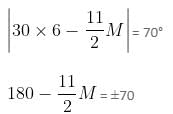
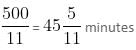
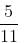
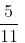 - 6:20 = 25
- 6:20 = 25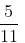 minutes
minutes










