Test Level 2: Mixtures and Alligations - 2 - CAT MCQ
15 Questions MCQ Test Level-wise Tests for CAT - Test Level 2: Mixtures and Alligations - 2
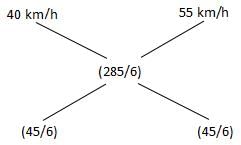
A bus driver is driving a bus at a speed of 40 km per hour. After travelling at this speed for some time, he increases its speed to 55 km per hour. If he travels a total distance of 285 km and the total time taken for the journey is 6 hours, then how much distance does he travel at the speed of 55 km per hour?
Three pots have the same volume. The ratio of milk and water in the first, second and third pots is 3 : 2, 7 : 3 and 11 : 4, respectively. What is the ratio of milk and water in the new mixture if liquids of the three pots are mixed?
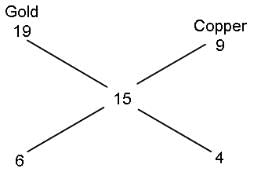
Gold is 19 times and copper is 9 times as heavy as water. In what ratio should these metals be mixed so that the mixture is 15 times as heavy as water?
A certain alloy contains 5 parts of A and 3 parts of B by weight. Another alloy contains 6 parts of A and 7 parts of B by weight. How much amount of A (in lbs) in its pure state must be melted along with 20 lbs of the first alloy and 65 lbs of the second so as to produce a new alloy containing 40% of B by weight?
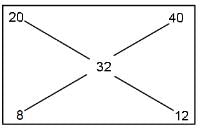
Kalicharan gets some coins made of an alloy of gold and silver. The alloy with a weight of 100 gm contains 20% of gold. What weight of another gold-silver alloy containing 60% of silver must be alloyed with the first piece of alloy in order to obtain a new alloy with 32% of gold?
A shopkeeper had 10 kg of rice, bought at the rate of Rs. 40 per kg and bought another 30 kg of rice at the rate of 20 per kg and mixed the two. At what price per kg should he sell the mixture to get 15% profit on the cost price?
Two equal containers are filled with a mixture of water and alcohol. One of them contains three times as much alcohol as the other. The mixtures in the two containers are then mixed and it is found that the ratio of water to alcohol is 3 : 2. Find the ratio of water to alcohol in each of the original containers.
A merchant buys a brand of tea at Rs. 80 per kg and mixes it with another brand bought at Rs. 140 per kg. He makes a profit of 25% on selling the mixture at Rs. 125 per kg. What is the ratio in which the brands are mixed?
A vessel contains 40 litres of milk. A milkman delivers 10 litres to the first house and adds an equal quantity of water. He does the same with the second and the third houses. What is the ratio of milk to water when he has finished delivering at the third house?
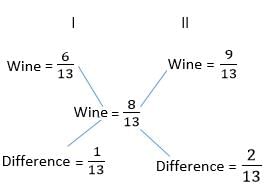
Cask I contains wine and water in the respective ratio 6 : 7 and cask II contains wine and water in the respective ratio 9 : 4. In what ratio must the contents of the two casks be mixed to get a mixture of wine and water in the respective ratio 8 : 5?
A container is full of sugar syrup. 4 gallons of syrup is drawn out of the container and replaced with water. From this water-syrup mixture, 4 gallons of mixture is again withdrawn and replaced with water. The ratio of the sugar syrup to water in the container was then found to be 36 : 13. How many gallons does the container hold?
We have three solutions of milk A, B and C. Solutions A, B and C contain milk and water in the ratios of 1 : 3, 2 : 3 and 3 : 2, respectively. If we mix them in the ratio 1 : 2 : 3, respectively, then what is the ratio of milk and water in the new solution?
Two metals X and Y are to be used for making two different alloys. If the ratio by weight of X : Y in the first alloy is 6 : 5 and that in the second is 7 : 13, then how many kilograms of X metal must be melted along with 11 kg of the first alloy and 20 kg of the second, so as to produce a new alloy containing 40% of metal Y?
A solution contains a mixture of liquid A and B in the ratio of 3 : 2. When 10 litre of solution is taken out and replaced by 10 litre of liquid B, the ratio of liquids A and B in the new solution is 1 : 2. What was the volume of the initial solution?
Two containers contain a mixture of milk and water. In one container, the ratio of milk to water is 4 : 1 and the ratio of milk to water in the other container is 1 : 3. 10 litres of mixture from the first container and 16 litres of mixture from the second container is mixed together in a third container, already containing some amount of pure milk. In the new mixture, it was found that the ratio of milk to water was 3 : 2. Find the volume of the new mixture.
|
5 docs|250 tests
|


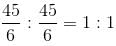
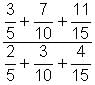 = 61 : 29
= 61 : 29
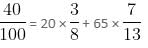
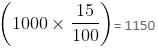
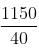 = = 28.75
= = 28.75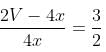
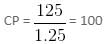
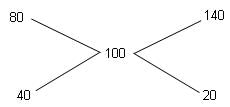
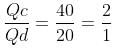
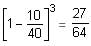
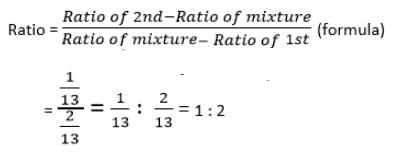
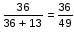 of the total volume of the container.
of the total volume of the container.
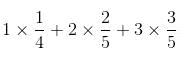 = 1/4 + 4/5 + 9/5 = (5 + 16 + 36)/20 = 57/20
= 1/4 + 4/5 + 9/5 = (5 + 16 + 36)/20 = 57/20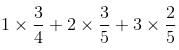 = 3/4 + 6/5 + 6/5 = (15 + 24 + 24)/20 = 63/20
= 3/4 + 6/5 + 6/5 = (15 + 24 + 24)/20 = 63/20 = 57 : 63 = 19 : 21
= 57 : 63 = 19 : 21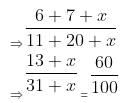
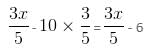
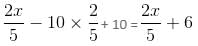
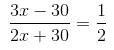
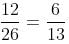
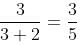
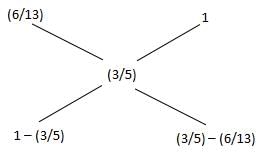
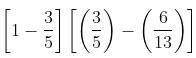 = 26 : 9
= 26 : 9















