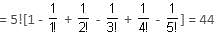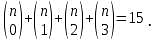Test Level 2: Permutation & Combination - 2 - CAT MCQ
20 Questions MCQ Test Level-wise Tests for CAT - Test Level 2: Permutation & Combination - 2
There are four rooms in a lodge: one single, one double, one for three persons and one for four persons. In how many ways can 10 persons be placed in these rooms?
There are 5 letters and 5 directed envelopes. The number of ways in which all the letters can be put in a wrong envelope are
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A five-digit number is formed by the digits 1, 2, 3, 4 and 5 without repetition. Find the probability that the number is divisible by 4.
How many five-digit numbers can be formed that are the same when the order of their digits is reversed?
A committee of four men and three women is to be formed from among six men and four women. If a particular woman, W1, refuses to be in the committee with another woman, W2, then in how many ways can the committee be formed?
A code is of the format XXXXYYYY, where X can be a letter from A-H and Y can be a digit from 0-9 such that no repetition of any letter or digit occurs (e.g. ABHE0387). How many such codes exist?
In an ice-cream store, one can pick from six flavours - Mango, Chocolate, Blueberry, Strawberry, Cherry and Vanilla. Further, one may also choose some topping from Choco-chip, Almond, Cashew, Pistachio and Coconut. One can even combine some or all of these toppings. How many different ice-creams are possible, if ice-cream of only one flavour can be chosen?
A city having eight hotels gets five tourists. In how many ways can these tourists stay in these hotels, if at least two tourists have to stay together?
How many five digit numbers contain exactly one 3?
There are 3 piles of identical red, blue and green balls and each pile contains at least 10 balls. The number of ways of selecting 10 balls, if twice as many red balls as green balls are to be selected, is
Seven distinct academic prizes are to be given to some students from a class of 50 students. Four prizes out of these are to be given to 4 distinct students. The rest three prizes can be given to any student even if he has won any other prize before. In how many ways can this be done?
The letters of the word RANDOM are written in all possible orders and the words so obtained are arranged in a dictionary order. In this list, the rank of the word RANDOM is
How many four-letter words can be formed if the first and the last letters are vowels (if repetition is allowed)?
In how many ways can two unit squares, 1 white and 1 black, be selected from an 8 x 8 chessboard such that they don't lie in the same row or column?
In an eating competition, Mr. Bhima has to eat 10 different sweets (one at a time) named A to J. In how many different ways can he eat all the sweets, such that he has to eat A before B and B before C?
How many four-lettered palindromes (same in both the directions), with or without meaning can be formed using the English alphabet?
There are 20 families with 4 members each, living in a 20-storey building. The families mutually decide to form a welfare committee for the well-being of all the residents. The committee will be of 10 members. Each family's only senior two members are eligible for membership in the committee and no more than 1 member from any family can be a part of the committee. In how many different ways can the committee be constituted?
How many 4-digit numbers divisible by 6 can be formed from the digits 1, 2, 3, 4, 5 and 6 without repetition?
How many natural numbers greater than 7,00,000 can be formed by using the digits 0, 3, 5, 6, 7, 8, if repetition is not allowed?
|
5 docs|272 tests
|