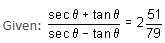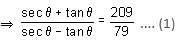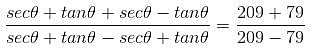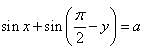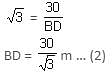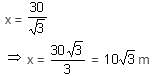Test Level 2: Trigonometry - 1 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 2: Trigonometry - 1
Find the value of (cosθ cos(90 - θ) secθ) ÷ (tanθ sin (90 - θ)).
If a = x sinθ + y cosθ and b = y sinθ - x cosθ, then y2 - a2 is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
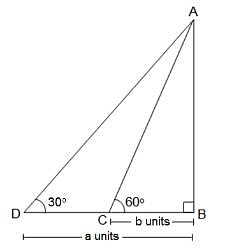
In the given figure, AB is the height of a tree. C and D are the two points in a straight line on the ground at b units and a units respectively away from the tree. What is the height of the tree (AB)?
A man on the top of a tower observes a car moving towards the base of the tower at an angle of depression α. Ten minutes later, the angle of depression of the car is found to be β. If the tangent of angle α. is equal to 1/√5, co-tangent of angle β is equal to 1/√5 and the car is moving with a uniform speed, find the total time taken by the car to reach the base of the tower.
The angles of elevation of the top of the tower, as observed from each of the points A, B and C on the ground, form a triangle at the same angle α. If R is the circum-radius of the triangle ABC, then the height of the tower is
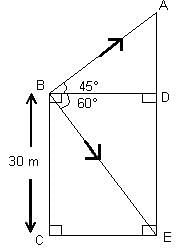
If sin x + cos y = a and cos x + sin y = b, then what will be the value of tan (x - y)/2 ?
A vertical building and a tower are on the same ground level. From the top of the building, the angle of elevation of the top of the tower is 45° and the angle of depression of the foot of the tower is 60°. Find the height of the tower, if the height of the building is 30 m.
|
5 docs|272 tests
|


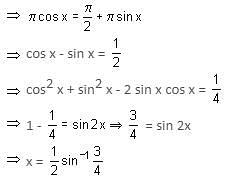

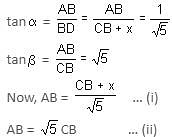

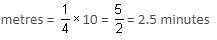
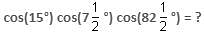
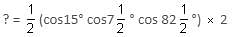
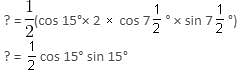

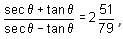 then the value of sin is
then the value of sin is