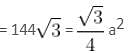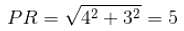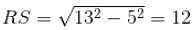Test Level 3: Geometry - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Geometry
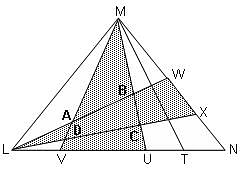
The area of triangle LMN is 120 square units. The shaded and unshaded regions have equal areas. If the area of triangle MVU is 1/3rd the area of triangle LMN, and the area of triangle LWX is 1/4th the area of triangle LMN, then find the area of quadrilateral ABCD. (Note: The figure is not drawn as per the scale.)

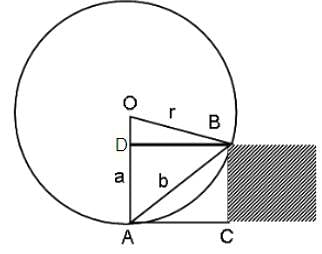
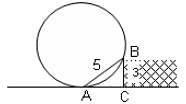
A wheel rests against the edge of a pavement as shown below. The height of the pavement is 3 m and the distance of the point where the wheel touches the ground from the point where the wheel touches the edge of the pavement is 5 m. Find the radius of the wheel.

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
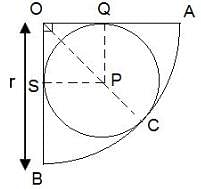
A circle is inscribed in a quadrant of a bigger circle, as shown in the figure below.

If the radius of the smaller circle is 2 units, what is the radius of the bigger circle?

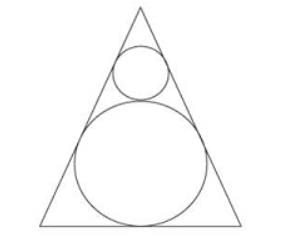
Two circles are placed in an equilateral triangle as shown in the figure. What is the ratio of the area of the smaller circle to that of the equilateral triangle
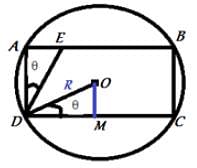
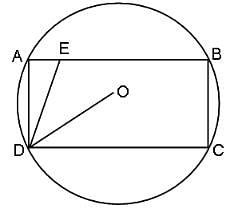
In the figure (not drawn to scale), rectangle ABCD is inscribed in a circle with centre at O. The length of side AB is greater than that of side BC. The ratio of the area of the circle to the area of the rectangle ABCD is π :. The line segment DE intersects AB at E such that ∠ODC = ∠ADE.
What is the ratio of AE : AD?
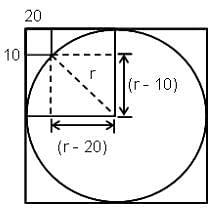
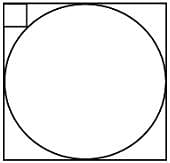
In the figure, the rectangle at the corner measures 10 cm x 20 cm. One corner of the rectangle is also a point on the circumference of the circle. What is the radius of the circle?
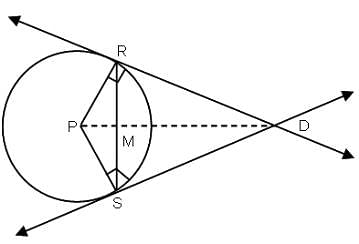
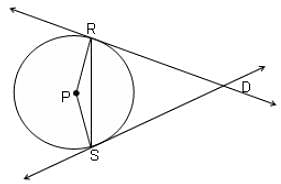
The area of an equilateral triangle DRS is 144√3 sq. cm. If P is the centre of the circle, find the area of quadrilateral DRPS in the given figure.
A, B, C, D, E ........ Z are the points marked on the circumference of a circle equidistantly. What can be the maximum number of triangles which can be formed using three points as vertices such that their circumcentre lies on one of the sides of a triangle?
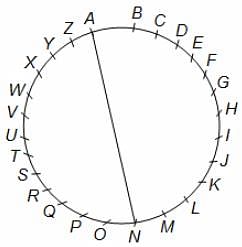
In the given figure, O is the centre of the circle and AE is a diameter. If AB = BC and ∠BFC = 25°, find the value of ∠ABC.

|
5 docs|272 tests
|