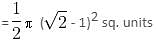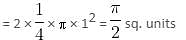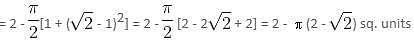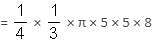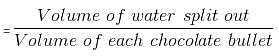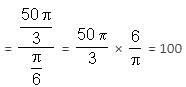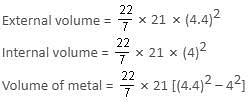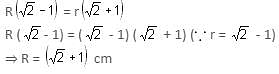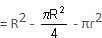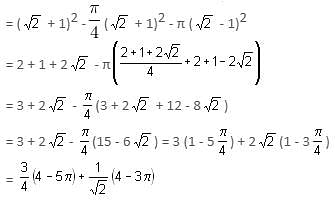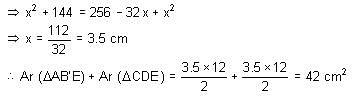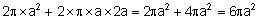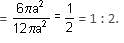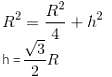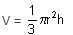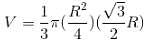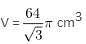Test Level 3: Mensuration - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Mensuration
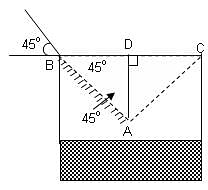
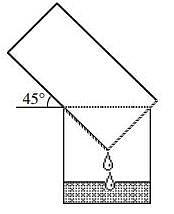
A cylindrical pail containing water drains into a cylindrical tub, 40 cm across and 50 cm deep, while resting at an angle of 45° to the horizontal, as shown in the figure. How deep is the water in the tub when its level reaches the pail?

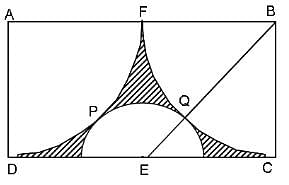
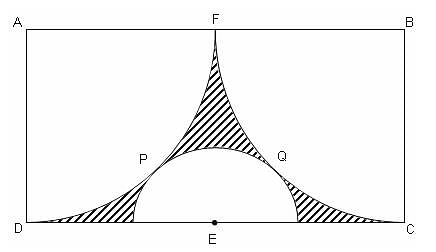
ABCD is a rectangle with AD = 1 unit. DPF and CQF are two equal arcs drawn with A and B as centres respectively. E is the midpoint of CD. Another arc with E as centre touches the two arcs DPF and CQF at P and Q, respectively. What is the area of the shaded portion?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cylindrical container, whose diameter is 12 cm and height is 15 cm, is filled with ice-cream. The whole ice-cream is distributed among 10 children in equal cones with hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream cone.
A vessel is in the form of an inverted cone, open at the top. Its depth is 8 cm and the diameter is 10 cm. It is filled with water up to the brim. When spherical chocolate bullets of radius 0.5 cm are dropped into the vessel, 1/4 of the water flows out. Find the number of bullets dropped in the vessel.
What will be the mass of a 21 cm long metallic hollow cylinder with internal diameter 8 cm and thickness of metal being 4 mm, if 1 cm3 of the metal weighs 8 gm?
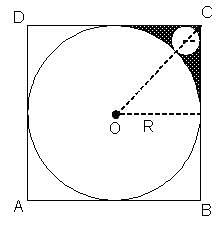
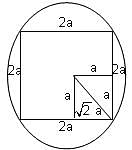
In the above figure, if the radius of the smaller circle is (√2 - 1) cm, then the area of the shaded region will be
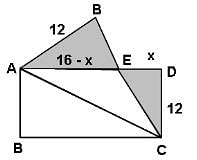
A rectangular piece of paper 16 cm long and 12 cm wide is folded along one of its diagonals. It results in some area of the paper doubling up over the portion of the paper already lying but some portion failing to double up, as it is not a square piece. Determine the area of the paper which has not doubled up.
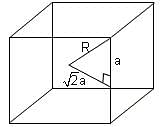
A cube of maximum possible volume is kept inside a sphere. A right circular cylinder of maximum possible volume is kept inside the cube. What is the ratio of the total outer surface area of the cylinder to that of the sphere?
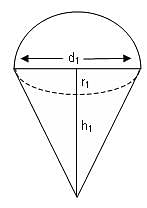
Ram cuts a semicircle of radius 8 cm from a piece of paper and folds it in such a way that it forms a right circular cone. What is the volume of this cone?
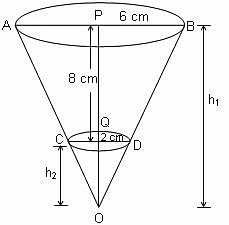
The height of a frustum made from a cone is 8 cm. If the base radii of this frustum are 6 cm and 2 cm, then find the height of the original cone.
|
5 docs|272 tests
|