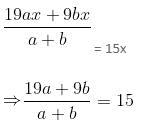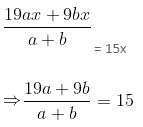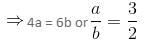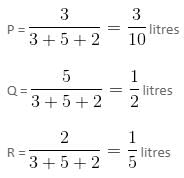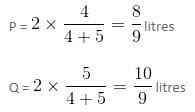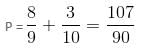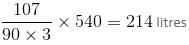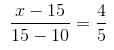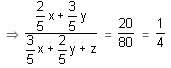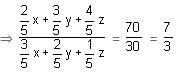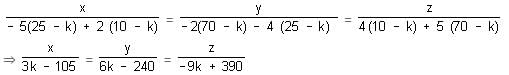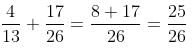Test Level 3: Mixtures and Alligations - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Mixtures and Alligations
Directions: Read the information given below and answer the question.
Sweetness of various items relative to sucrose, whose sweetness is taken as 1, is:
Lactose: 0.16, Maltose: 0.32, Glucose: 0.74, Sucrose: 1.00, Fructose: 1.70, Saccharin: 675.00
Approximately how many times is sucrose sweeter than a mixture consisting of glucose, sucrose and fructose in the ratio 1 : 2 : 3?
Sweetness of various items relative to sucrose, whose sweetness is taken as 1, is:
Lactose: 0.16, Maltose: 0.32, Glucose: 0.74, Sucrose: 1.00, Fructose: 1.70, Saccharin: 675.00
Approximately how many times is sucrose sweeter than a mixture consisting of glucose, sucrose and fructose in the ratio 1 : 2 : 3?
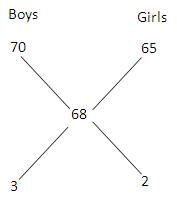
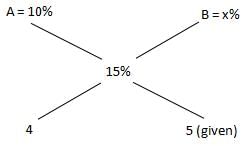
A total of 750 candidates appeared in an examination. 70% of the boys and 65% of the girls passed the examination. If the total pass percentage was 68%, find the number of boys who appeared in the examination.
Gold is 19 times as heavy as water and copper is 9 times as heavy as water. In what respective ratio should these metals be mixed, so that the mixture is 15 times as heavy as water?
Mixtures A and B are contained in two separate vessels. Mixture A contains ingredients P, Q and R in a ratio of 3 : 5 : 2 and mixture B contains ingredients P and Q in a ratio of 4 : 5. We have to make 540 litres of a new mixture by adding the mixtures A and B in a ratio of 1 : 2. What will be the quantity of ingredient P in the final mixture?
The weights of two boxes A and B containing sugar are in the ratio 4 : 5. Some amount of sugar is added to both the boxes and it is found that the weight of box A increases by 10% and the total weight of boxes A and B together becomes 82.8 kg. If this weight is 15% more than the previous weight, then find the percentage with which the weight of box B increases.
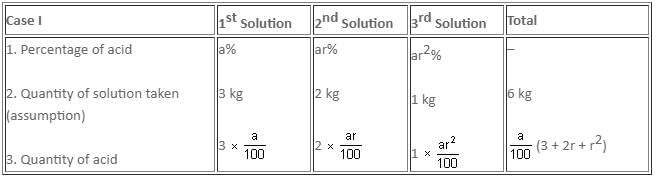
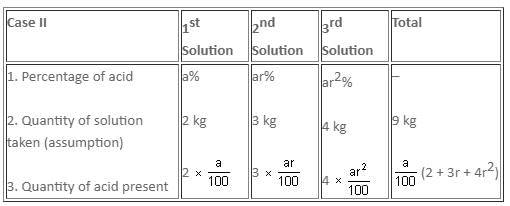
The percentage amounts of an acid in three solutions form a geometric progression. If we mix the first, second and third solutions in the ratio 3 : 2 : 1 by weight, we get a solution containing 22% acid. On the other hand, if we mix the solutions in the ratio 2 : 3 : 4 by weight, we obtain a solution containing 32% acid. Find the percentage of acid in each solution.
There are two solutions of HCl in water. The first is 40% strong and the second is 60% strong. The two solutions are mixed. Some amount of pure water is added and a 20% strong solution is obtained. If instead of adding pure water, the same amount of an 80% strong solution had been added to the mixture, then a 70% strong solution would have been obtained. What was the initial quantity of the 40% and the 60% solutions?
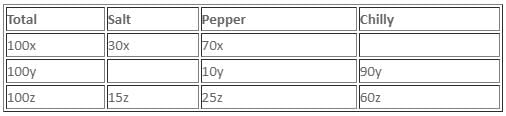
There are three mixtures. The first mixture contains 30% salt and 70% pepper, the second contains 10% pepper and 90% chilly, and the third contains 15% salt, 60% chilly and the rest pepper. They are mixed to obtain a new mixture which contains 40% chilly. The percentage of pepper in the new mixture cannot be more than
There are two qualities of gold alloys 22 carat and 23 carat having different prices per gram, their volumes being 130 gm and 180 gm, respectively. After equal quantities were taken from both the alloys, the alloy removed from the 22-carat alloy was added to the 23-carat alloy and vice versa. The resulting two types of alloys now have the same price per gram. Find the quantity of alloy drawn out from each type. It is to be assumed that 100% gold is 24 carats.
P and Q are two different mouth fresheners, prepared by mixing supari and saunf in the proportions 9 : 4 and 9 : 17, respectively. If equal quantities of the mouth fresheners are mixed to form a third kind of mouth freshener R, find the ratio of saunf to supari in R.
|
5 docs|250 tests
|