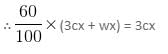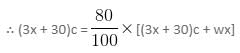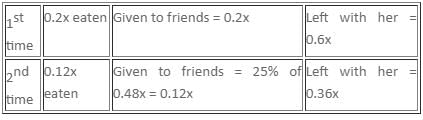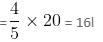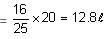Test Level 3: Percentages - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Percentages
If a quantity A is successively increased by 20% for two times and another quantity B is successively increased by 10% for three times, then quantity A becomes 80% of quantity B. What percentage is the original value of quantity A as compared to the original value of quantity B?
In an election, 3/5th of the voters promised to vote for X and the rest promised to vote for Y. Out of these, on the last day, 15% of the voters of X went back on their promise to vote for X and instead voted for Y. 25% of the voters of Y went back on their promise to vote for Y and voted for X instead. X won by 22 votes. The total number of votes for X is
If the price of ice cream increases by a quarter and Vaibhav intends to spend only an additional fifteen percent on it, by how much percentage will he reduce the quantity of ice cream purchased?
A company has raised seventy-five percent of the amount it needs for a new project by receiving an average amount of Rs. 600 from persons already associated. The already associated people represent 60% of the people from which the company will ask for the money. If the company needs exactly the same amount it needs for the project, then what is the average money it will get from the remaining people?
In a group of p friends, x% have both credit cards and mobile phones. Out of p, y% of the males and z% of the females have both credit cards and mobile phones. Find the number of males in the group in terms of p, x, y and z.
Two candidates were contesting for the post of Rotary Club chairman. In the first round of voting, 550 members participated. In the second round, again 550 members participated. However, the number of members opposed to the first candidate increased by 150% and the combined votes of the first candidate (for both the rounds) exceeded that of the second by 400. How many members opposed the first candidate in the first round? No votes were invalid.
In an exhibition, 60% of the collection is from the sales of cold drinks and rest is from the sales of water bottles. Had 30 more cold drinks been sold, their contribution would have been 80%. If the number of water bottles sold is 1/3rd of the number of cold drinks sold, find the total number of cold drinks sold.
Padma purchased a box of chocolates. She ate 20% of them and gave 25% of the remaining chocolates to her friends. Again, she ate 20% of it and gave 25% of the remaining chocolates to her friends. Then, she gave 8 chocolates to a guest. Finally, she is left with 35% of the chocolates that she initially had. How many chocolates did Padma eat?
In a container having milk, 20% milk is replaced by water and this process is repeated thrice. At the end of the third operation, the percentage of pure milk in the container is
A motorist uses 24% of his fuel in covering the first 20% of his total journey (in city driving conditions). He has to cover another 25% of his total journey in city driving conditions. What should be the minimum percentage increase in fuel efficiency for non-city driving over that in city driving, so that he is just able to cover his entire journey without having to refuel?
|
5 docs|250 tests
|