Test Level 3: Permutation & Combination - 1 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Permutation & Combination - 1
How many ways are there to pick two different cards from a deck of 52 cards such that the first card is
(a) an ace and the second is not a queen
(b) a spade and the second is not a queen
(a) an ace and the second is not a queen
(b) a spade and the second is not a queen
How many 4-digit numbers can be formed by using the digits 0, 2, 3, 5 and 8 (without repetition), such that each number is not divisible by 4?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In how many ways can 4 cards be drawn randomly from a pack of 52 cards such that there are at least 2 kings and at least 1 queen among them?
The manager of a football team of eleven players wants to take photographs of his team, six players at a time. He can choose any one out of four renowned photographers to take the photographs. In how many ways can the photographs be taken, if the Captain and the Vice-Captain of the team are always included in the photographs? Also, find out the number of ways in which the photographs can be taken, if the Captain and the Vice-Captain of the team are never included in the photographs.
A 6-character code is made of only 0s and 1s, such that the number of 0's is always greater than the number of 1's. How many such codes exist?
A club has 15 members; 12 of them being married couples and 3 being unmarried. These members have decided to form a leadership board in the club which consists of 4 members: President, Vice-president, Public Relations Officer and General Manager. The Public Relations Officer is to be selected from the unmarried members. For all the other positions, the member selected has to be married. However, one couple decides that they both together will not be a part of the leadership board. In how many ways can the board be formed?
Six cards are to be selected from a deck of cards. At least 1 card is to be selected from each suit. In how many different ways can this be done?
Two groups are to be formed from 10 different boys of a class. The groups may or may not be of the same size. In how many different ways can this be done?
Some tennis balls are to be put into 7 boxes such that each box contains at least one ball. At the most, 3 of the boxes are to contain the same number of balls, and no two of the remaining boxes are to contain an equal number of balls. What is the least possible number of tennis balls needed for the boxes?
In how many ways can 9 blocks of 3 different colours and 3 different sizes, where all blocks of a particular colour have different sizes, be arranged in a straight line such that blocks of the same colour sit together, and at the point where the colour changes, the adjoining blocks are the same size?
|
5 docs|272 tests
|


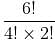 = 15 (4! is divided as 0 repeats 4 times and 2! is divided as 1 repeats two times)
= 15 (4! is divided as 0 repeats 4 times and 2! is divided as 1 repeats two times)














