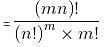Test Level 3: Permutation & Combination - 2 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Permutation & Combination - 2
A married couple invites two other married couples for a round-table dinner party. In how many ways can they be seated if each one sits diametrically opposite to his/her spouse?
There are 3 ways from a town A to reach town B, 4 ways from town B to reach town C, and 2 ways from town A to reach town C directly. In how many ways can a person go from town A to town C and then return to A, if he does not take the way already taken?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Four departments in an engineering college (ME, PE, CE and EE) contain 4 faculty members each, i.e. an HOD, an Associate Professor, an Assistant Professor and a Lecturer. Each department also has 5 student coordinators. A panel of 4 members is to be constituted for a conference such that 1 faculty member is selected from each department, so that the final committee has an HOD, an Associate Professor, an Assistant Professor and a Lecturer. Also, 10 student coordinators have to be selected and no restrictions exist for the selection of the student coordinators. In how many ways can the panel be constituted including the selection of the student coordinators?
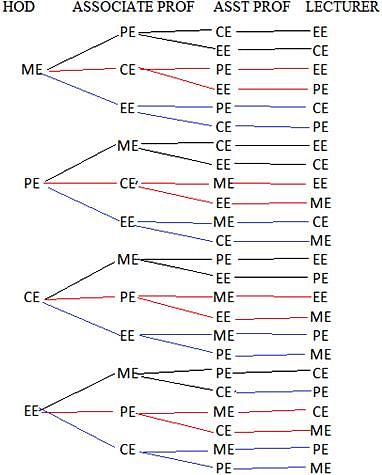
From the 7 HODs of seven departments of an engineering college, one is to be promoted to be the principal of the college. Further, the position which is now vacant for the HOD is to be filled by an Associate Professor being promoted as an HOD. And further, one Assistant Professor is to be promoted to be an Associate Professor. No further promotions are made. The number of Associate Professors in the college is 4, 5, 3, 5, 2, 1 and 4 and that of Assistant Professors is 8, 9, 12, 5, 6, 7 and 6 for the departments of Mechanical, Electrical, Electronics, Civil, Chemical, Computer Science and Production Engineering, respectively. In how many different ways can the changes occur?
In a game, a person has to select three cards from a deck of cards. If he selects a face card, then the other two cards also have to be face cards. If a number card is selected, then all the other cards have to of the same number. In how many different ways can the selection be made?
On a plane paper, 11 dots are marked. Out of these dots, only 5 lie in a straight line. Rest of them are haphazardly spread out throughout the paper. How many unique triangles can be formed by joining them?
How many different kinds of necklaces can be made containing 3 beads each from 3 white beads, 3 black beads and 3 red beads?
A married couple invites 6 other couples for a dinner party. They are seated around a long table with one seat each at the short ends of the table and 6 seats each at either long side. In how many ways can they be seated if the hosts sit at the short ends and the other guests are free to sit anywhere?
The number of words formed by arranging all the letters in the word EDUCATION, such that the letters CAT appear in the same place as in the given word and no vowels come together, is
If w represents the cube root of unity, then the number of values of (p, q, r), such that wp + wq + wr = 0, where p, q and r are positive integers less than 9, is
|
5 docs|272 tests
|