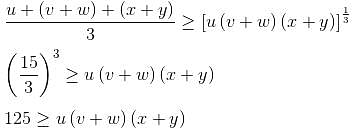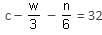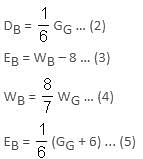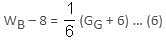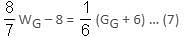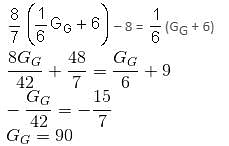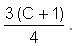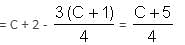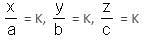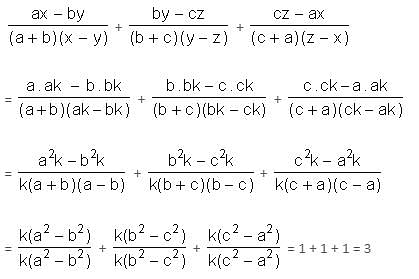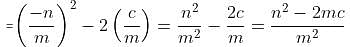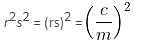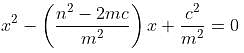Test Level 3: Quadratic Equations & Linear Equations - CAT MCQ
15 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Quadratic Equations & Linear Equations
If u + v + w + x + y = 15, then what is the maximum value of uvx + uvy + uwx + uwy?
Which of the following relationships is correct, if α and β are the roots of |x|2 + |x| - 6 = 0?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the minimum value of f(x) = x2 + 2bx + 2c2 is greater than the maximum value of g(x) = -x2 - 2cx + b2, then (x being real)
The values of a for which one root of the equation x2 - (a + 1)x + a2 + a - 8 = 0 exceeds 2 and the other is less than 2, are given by
A test has 50 questions. A student scores 1 mark for a correct answer, –1/3 for a wrong answer and –1/6 for not attempting a question. If the net score of a student is 32, then the number of questions answered wrongly by that student cannot be less than
Which of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has at least one solution, such that p + q + r ≠ 0?
x + 2y - 3z = p
2x + 6y - 11z = q
x - 2y + 7z = r
Ghosh Babu said to Banke Lal, "My wife is six years older than your daughter. Your daughter is one-sixth the age of my great-grandfather. But, your eldest son is younger than your second wife by eight years." Banke Lal replied, "My second wife is older than your only wife by one-seventh. My eldest son is one-sixth the age of what your great-grandfather would have been today, had he not died six years ago.'' What would have been the age of Ghosh Babu's great-grandfather at the time of this conversation?
Four dog dealers purchased some dogs. The first dealer purchased 1 Airedale, 3 Spaniels and 7 puppies and paid $1400; and the second purchased 1 Airedale, 4 Spaniels and 10 puppies and paid $1700. The third purchased 10 Airedales, 15 Spaniels and 25 puppies; and the fourth purchased 1 Airedale, 1 Spaniel and only 1 puppy. How much did the third and fourth dealers pay, separately?
Three drunkards agreed to pool their vodka and decided to share it with the fourth drunkard (who had no vodka) at a price equal to 5 roubles a litre. The first drunkard contributed 1 litre more than the second and the second contributed 1 litre more than the third. Then, all four of them divided the vodka equally and drank it. The fourth drunkard paid money, which was divided in the ratio of each drunkard's contribution towards his portion. It was found that the first drunkard got twice as much money as the second. How much money did the second drunkard get (in roubles)?
Rocky and Anthony are solving a quadratic equation. While solving, Rocky commits a mistake in the constant term and finds the roots to be 8 and 2. Anthony commits a mistake in the coefficient of X and finds the roots to be -9 and -1. Find the correct roots.
If r and s are the solutions of quadratic equation mx2 + nx + c = 0, which of the following equations can have its roots equal to r2 and s2?
It is known that y2 - 11y + 4k = 0 has two distinct roots. It is also known that one factor is (y - k) and k is greater than zero. What is the difference between the sum and products of the roots?
A harvester's team had to harvest 170 hectares of a field. For the first four days, the team harvested as per the plan. After that, they started harvesting at double the rate planned for every day. So, the work was finished eight days before the planned date. How many hectares had to be harvested by the team each day as per the initial plan?
36 coins are divided among A, B, C and D, such that B takes more than A, C takes more than B and D takes more than C. If the difference in the number of coins between A and B is 1, between B and C is 9 and between C and D is 7, the number of coins with A is
|
5 docs|272 tests
|