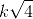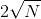Test Level 3: Ratio & Proportion - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Ratio & Proportion
Two persons are awarded pensions in proportion to the square root of the number of years they have served. The second person's service period is 9 years longer than that of the first. If the length of service of the first person had exceeded that of the second by 4.25 years, their pensions would have been in the respective ratio of 9 : 8. How long have the two served?
The monthly incomes of Vasu and Ravi are in the ratio 7 : 8 and their monthly expenditures are in the ratio 3 : 4, respectively. If the respective savings of Vasu and Ravi are Rs. 2,400 and Rs. 1,600, then find the monthly income of Ravi.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Suman began a business with a capital of Rs. 50,000 and after 3 months, Manu entered into the partnership with a capital of Rs. 75,000. Three months later, Amandeep joined the firm with a capital of Rs. 1,25,000. At the end of the year, the firm made a profit of Rs. 99,495. How much of this sum did Amandeep receive?
The only people in each of the auditoriums A and B in a school are students, and each student in each of the auditoriums A and B is either from Grade 8 or from Grade 7. The ratio of number of students from Grade 8 to those from Grade 7 in auditorium A is 4 : 5. The ratio of number of students from Grade 8 to those from Grade 7 in auditorium B is 3 : 17, and the ratio of the total number of students from Grade 8 in both auditoriums to the total number of students from Grade 7 in both auditoriums A and B is 5 : 7. What is the ratio of the total number of students in auditorium A to the total number of students in auditorium B?
Three friends count the number of coins they have. They found that the ratio of the total number of coins of 25 p, 50 p and Re 1 is 11 : 6 : 13. They have 25 p coins in the ratio 2 : 4 : 5, 50 p coins in the ratio 6 : 3 : 9 and Re 1 coins in the ratio 7 : 2 : 4. Find the amount with the second person, if they have money only in the denomination of 25 p, 50 p and Re 1 and the total number of 25 p coins with them is 132.
A balloon can go up in the air at the rate of 24 kmph and its speed diminishes by a quantity, which varies as the square root of the number of stones attached to it. With four stones, its speed is 20 kmph. The highest number of stones with which the balloon can go up in the air is
Tanya and Sanya invested some amount of money in the ratio 7 : 6 for the same period. At the end of the year, 20% of the profit was donated to an old age home. Out of the remaining profit, 50% is reinvested and the rest is divided in the ratio of their initial contribution. If the difference between their shares of profit is Rs. 4400, what was the total profit?
Three persons Akbar, Birbal and Tansen invested in a business Rs. 10,000, Rs. 25,000 and Rs. P, respectively. Akbar withdrew Rs. 1,000 after 3 months and Rs. 1000 again after 5 months. Birbal invested Rs. 7,000 more than his initial investment after 9 months. Tansen maintained his capital for the whole year. If at the end of the year, they made a profit of Rs. 12,400, and Tansen got Rs. 2,400 as his share in the profit, find the initial investment made by Tansen.
Mr. Alaram designed a new clock, which has 12 divisions as usual, represented by the numbers 1 to 12. But the speed of the minute hand is directly proportional to the digit, which it is going to approach, i.e. if the minute hand is between 1 and 2, its speed is proportional to 2 and if it is between 11 and 12, its speed is proportional to 12. The speed of the minute hand, when it is between 12 and 1 is equal to that of an ordinary clock and both the clocks were set at 9 : 00 am.
What will be the time in the ordinary clock, if the new clock shows 9 : 30 am?
Amounts deposited by two friends Harpreet and Gagan are in the ratio 7 : 9. Total amount deposited is Rs. 72,000. After some time, Harpreet withdraws Rs. 7500. Find the money withdrawn by Gagan, so that the new ratio of their deposits may become 4 : 5.
|
5 docs|272 tests
|


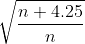 =
= 
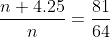
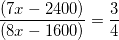
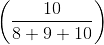 × 99,495 =
× 99,495 = 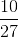 × 99,495 = Rs. 36,850
× 99,495 = Rs. 36,850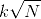 (where k is proportionality constant)
(where k is proportionality constant)