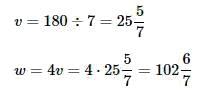Test: Line And Angles - GMAT MCQ
15 Questions MCQ Test - Test: Line And Angles
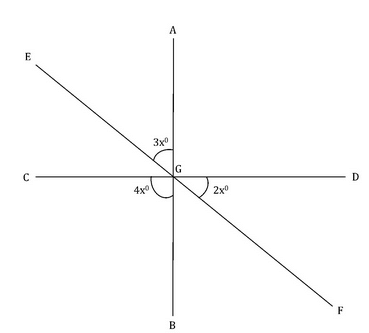
AB, CD and EF are three line segments intersecting at a common point G as shown in the given figure. Find the value of ∠CGB.
If two complementary angles are in the ratio 13:5, then the angles are ________.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the given figure, BC and EF are line segments intersecting at F. FD and AF are the angle bisectors of ∠EFC and ∠EFB respectively. Find the value ∠AFE + ∠DFE.
In the given diagram, line segment EF and BC are parallel to each other. Find the value of (x+y).
Three parallel lines l1, l2 and l3 are intersected by two parallel transversals m1 and m2. What is the measure of angle y?
If the lines l1 and l2 are parallel to each other, and the transversal line m intersects it such that ∠PRS= 3a and ∠RYX= 6b, then what is the value of “a + 2b” ?
In the given figure, three angles X, Y, and Z are formed at the centre O of the circle. If the angles X, Y, and Z are in the ratio 1:3:5 respectively, then find the value of Y.
In the figure above, AOD is a straight line. Find the measure of ∠AOB
In the given figure, if the lines l1 and l2 are parallel to each other, and the transversal line m intersects it. What is the value of y?
In the given figure, what is the value of a + b, if both a and b are positive integers?
In the figure above, AD bisects angle BAE and AE bisects angle CAD. Also, the line XY and AC are parallel to each other. Find the value of ∠DAE
.
(1) ∠BAC = 60o
(2) ∠XOB = 120
Is the segment CD a perpendicular bisector of the segment AB?
(1) Half of CD = CO
(2) AO = DO
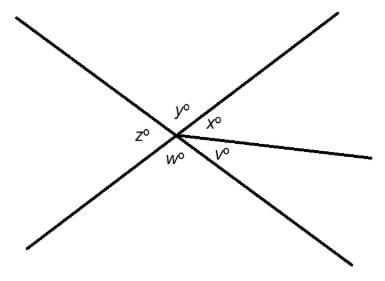
Refer to the above diagram. Evaluate w.
Statement 1: x=2v
Statement 2: y=2x
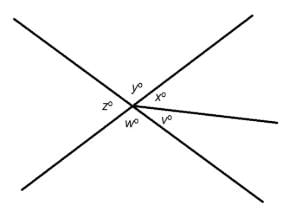
Refer to the above diagram. Evaluate v.
Statement 1: x+y=150
Statement 2: w+v=130