Test: Linear Algebra- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Linear Algebra- 1
Let A be an mxn matrix and B an n*m matrix.
It is given that determinant (Im + AB) = determinant (In + BA) , where Ik is the k*k identity matrix. Using the above property, the determinant of the matrix given below is

It is given that determinant (Im + AB) = determinant (In + BA) , where Ik is the k*k identity matrix. Using the above property, the determinant of the matrix given below is
The matrix of coefficients either have no solution or have infinite solutions is system of equations are
If the matrix A is such that
then the determinant of is equal to ______.
Two eigenvalues of a 3 x 3 real matrix P are (2 + √-1) and 3 . The determinant of P is _______
Suppose that the eigenvalues of matrix A are 1,2, 4. The determinant of (A-1)T is _______________.
In the given matrix, one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
Consider the following 2×2 matrix A where two elements are unknown and are marked by a and b. The eigenvalues of this matrix are -1 and 7. What are the values of a and b?
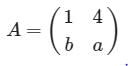
The value of the dot product of the eigenvectors corresponding to any pair of different eigenvalues of a 4 - by - 4 symmetric positive definite matrix is ___________
real valued square symmetric matrix of rank
Consider the following statements.
(I) One eigenvalue must be in
(II) The eigenvalue with the largest magnitude must be strictly greater than 5
Which of the above statements about eigenvalues of is/are necessarily CORRECT?
Let A be the matrixWhat is the maximum value of xT Ax where the maximum is taken over all x that are the unit eigenvectors of A?
Let A be a matrix with eigen values -5,-2,1,4. Which of the following is an eigen value of the matrix
, where
identity matrix?
Consider the matrix as given below.
Which one of the following options provides the CORRECT values of the eigenvalues of the matrix?
Which one of the following statements is TRUE about every matrix with only real eigenvalues?
The product of the non-zero eigenvalues of the matrix is ____
If the characteristic polynomial of a (the set of real numbers) is
and one eigenvalue of M is 2, then the largest among the absolute values of the eigenvalues of M is _______