Test: Linear Programming Level - 3 - Mechanical Engineering MCQ
14 Questions MCQ Test - Test: Linear Programming Level - 3
Max z = 40x1 + 60x2
s/t: 2x + y ≤ 90
x + y ≤ 50
x + 2y ≤ 80
x, y ≥ 0
Find the value of zmax
Solve the following LPP and identify the type of solution
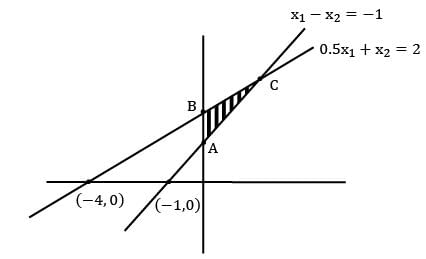
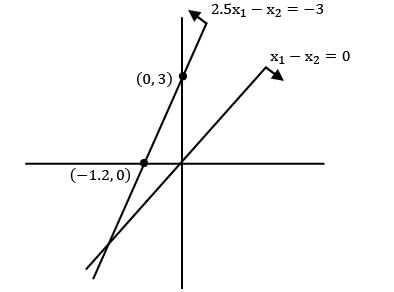
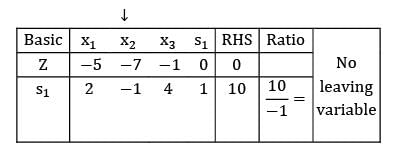
Max z = 3x1 + 4x2
s/t: x1 − x2 ≥ 0
2.5x1 − x2 ≤ −3
x1 , x2 ≥ 0
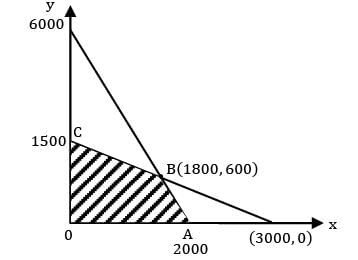
A company produces cups and trays by deep drawing and forming operations. Following data is given on capacity availability and economics of each product.
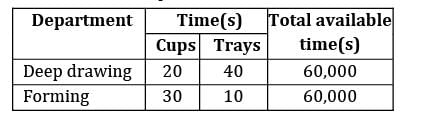
The profit on each cup and tray is given as Rs.40 and Rs.80 respectively. Total daily fixed cost is Rs.90, 000. The maximum net profit per day at the optimum production level is ____________ Rs. [Consider the effect of fixed cost also]

Consider the following LPP
Max z = 2x1 + 10x2
s/t: 3x1 + 2x2 ≤ 4
5x1 + 3x2 ≤ 6
x1 + x2 ≤ 10
The solution for the above LPP is
Consider the following LPP
Minimize z = 5x1 + 7x2 + x3
s/t: 2x1 − x2 + 4x3 ≤ 10
x1 , x2 , x3 ≥ 0
The solution for the above LPP is
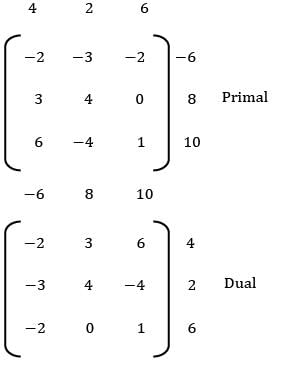
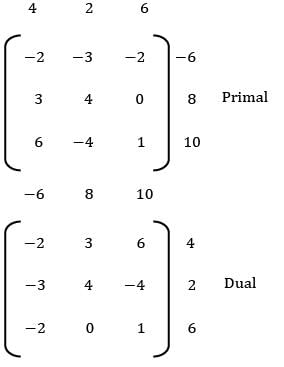
Consider the following primal LPP. Find dual of the given primal.
Max: z = 4x1 + 2x2 + 6x3
s/t: 2x1 + 3x2 + 2x3 ≥ 6
3x1 + 4x2 ≤ 8
6x1 − 4x2 + x3 ≤ 10
s/ t: 2y1 + 3y2 + 6y3 ≥ 4
3y1 + 4y2 − 4y3 ≥ 2
2y1 + y3 ≥ 6
y1 , y2, y3 ≥ 0
s/t: − 2y1 + 3y2 + 6y3 ≥ 4
−3y1 + 4y2 − 4y3 ≥ 2
−2y1 + y3 ≥ 6
y1 , y2, y3 ≥ 0
2y1 + 3y2 + 6y3 ≤ 4
3y1 + 4y2 − 4y3 ≤ 2
2y1 + y3 ≤ 6
y1 , y2, y3 ≥ 0
s/t: − 2y1 + 3y2 + 6y3 ≤ 4
−3y1 + 4y2 − 4y3 ≤ 2
−2y1 + y3 ≤ 6
y1 , y2, y3 ≥ 0
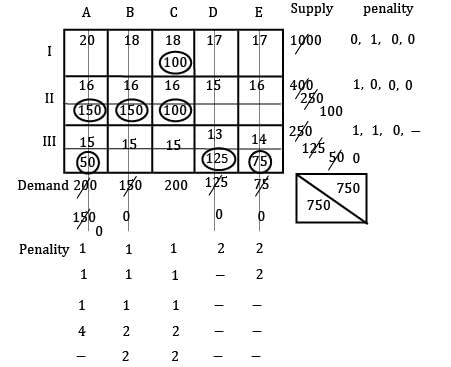
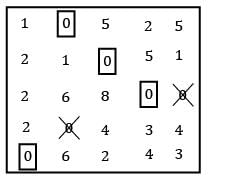
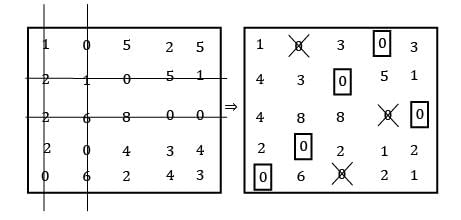
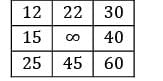
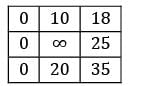
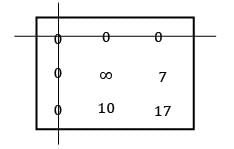
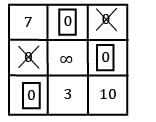
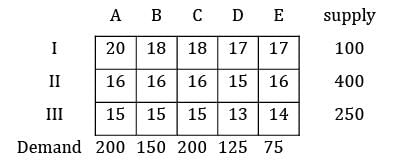
Find the initial basic feasible solution using VAM method.
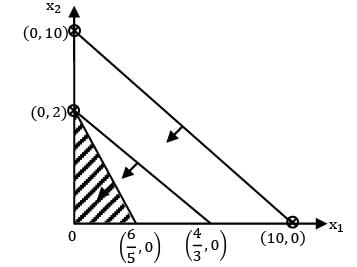
A product is manufactured using two raw materials A and B. A is taken on x-axis and B is taken on Y-axis and the LPP is as follows.
Zmin = 2A + 3B
S⁄t ∶ 0.6 A + 0.3 B ≥ 45
0.1 A + 0.5B ≥ 25
A, B ≥ 0
Which of the following statement is correct?
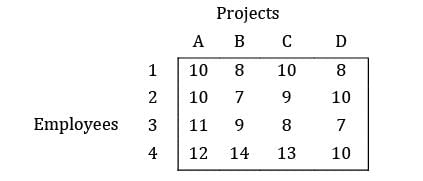
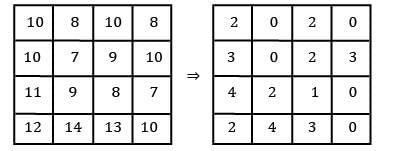
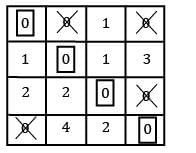
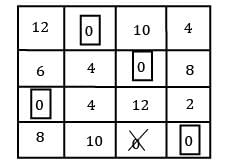
Four workers are required to do four jobs. Time to complete every job is given in the table below

Find the minimum cost.
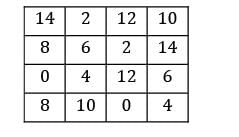
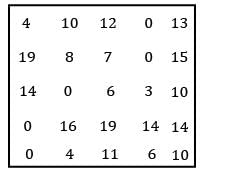
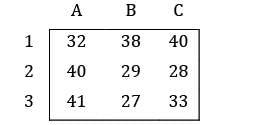
Consider the following profit matrix. Find the max profit
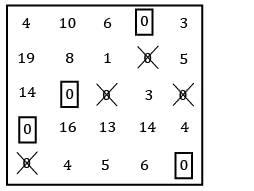
Consider the problem of assigning four sales persons to four different sales regions as given below. Find the maximum total sales?
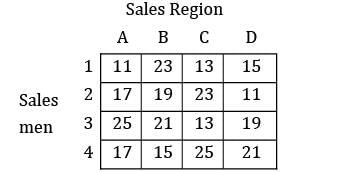
All the values are given in thousands.
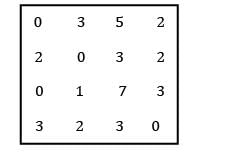
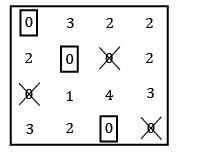
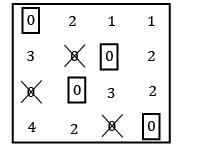
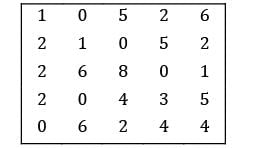
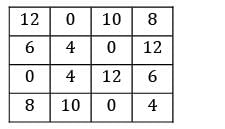
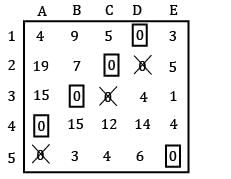
Consider the following problem A cost matrix is given, find the minimum total cost
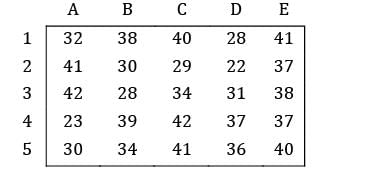
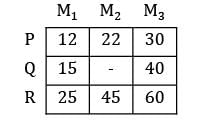
Three workers (P, Q, R) are assigned to 3 machines (M1 , M2 , M3 ) while operator Q cannot be assigned machine M2 . Further, each operator is assigned to one machine and one machine requires only one operator. The operating cost is given for these operators in table below (in Rs). The minimum cost of assignment is ___________ (Rs).