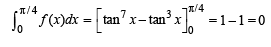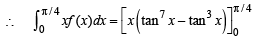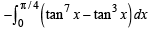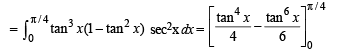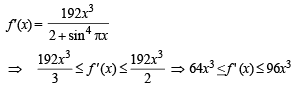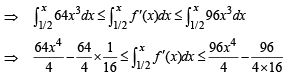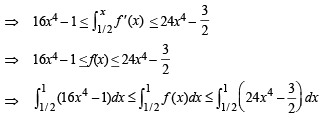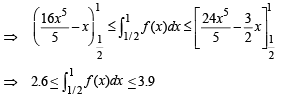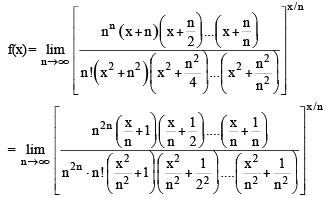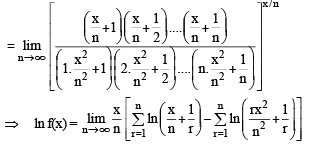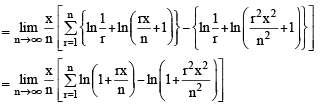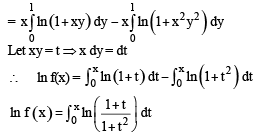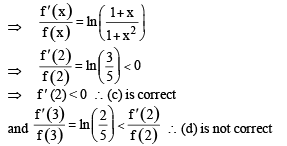Test: MCQs (One or More Correct Option): Definite Integrals and Applications of Integrals | JEE Advanced - Airforce X Y / Indian Navy SSR MCQ
13 Questions MCQ Test Mathematics for Airmen Group X - Test: MCQs (One or More Correct Option): Definite Integrals and Applications of Integrals | JEE Advanced

Let f(x) = x – [x], for every real number x, where [x] is the integral part of x. Then 

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
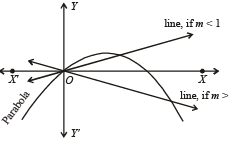
For which of the following values of m, is the area of the region bounded by the curve y = x – x2 and the line y = mx equals 9/2?
Let f (x) be a non-constant twice differentiable function definied on ( -∞,∞) such th at f (x) = f (1 – x) and 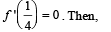
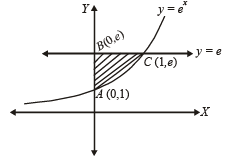
Area of the region bounded by the curve y = ex and lines x = 0 and y = e is
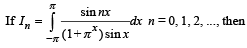
The value(s) of 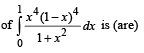
Let f be a real-valued function defined on the interval (0, ∞) by 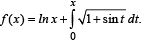 Then which of the following statement(s) is (are) true?
Then which of the following statement(s) is (are) true?
Let S be the area of the region enclosed by 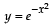 , y = 0, x = 0 and x = 1; then
, y = 0, x = 0 and x = 1; then
The option(s) with the values of a and L that satisfy the following equation is(are) 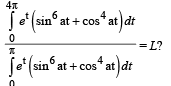
Let f(x) = 7tan8x + 7tan6x – 3tan4x – 3tan2x for all 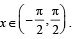 Then the correct expression(s) is(are)
Then the correct expression(s) is(are)
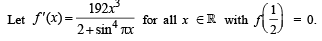
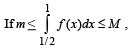 then the possible values of m and M are
then the possible values of m and M are
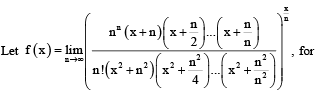 all x > 0. Then
all x > 0. Then
|
149 videos|192 docs|197 tests
|
|
149 videos|192 docs|197 tests
|


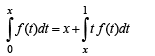

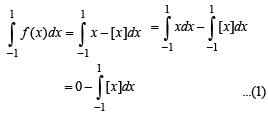
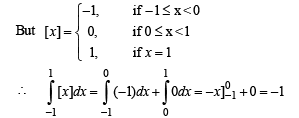
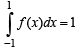
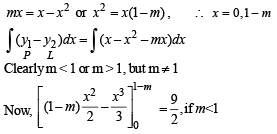
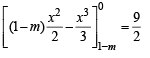
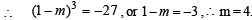
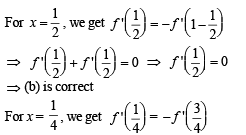
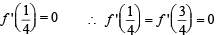
 So there exists at least one point
So there exists at least one point 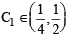 and at least one point
and at least one point 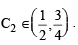
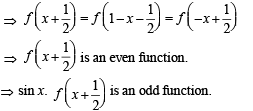
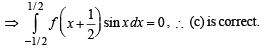
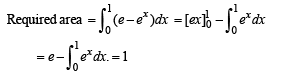
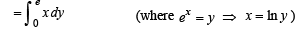
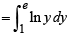
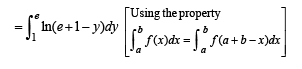
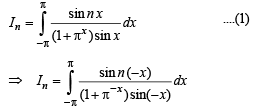
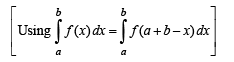
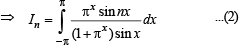
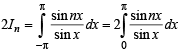 [as integrand is an even function]
[as integrand is an even function]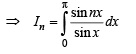
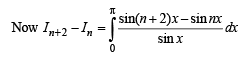
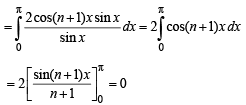
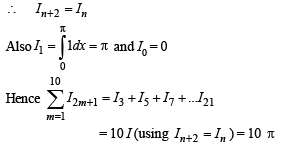
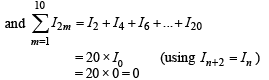
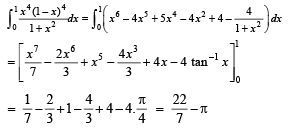
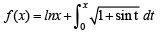
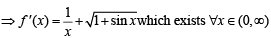
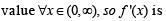 continuous
continuous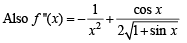
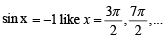
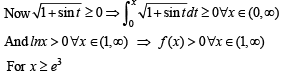
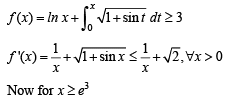
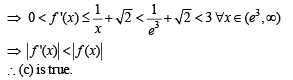
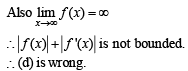
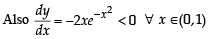
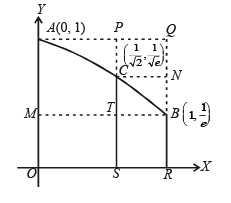
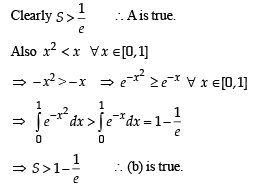
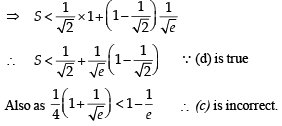
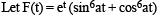

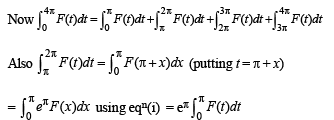
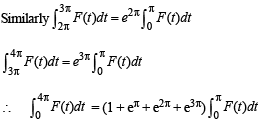
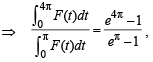 where ‘a’ can take any even
where ‘a’ can take any even