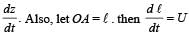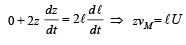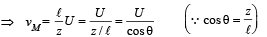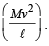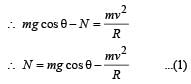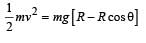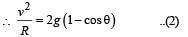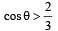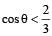Test: MCQs (One or More Correct Option): Laws of Motion | JEE Advanced
6 Questions MCQ Test Physics 35 Years JEE Main & Advanced Past year Papers | Test: MCQs (One or More Correct Option): Laws of Motion | JEE Advanced
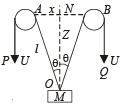
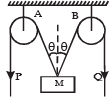
In the arrangement shown in the Fig, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed.
Mass M moves upwards with a speed
This is a problem based on constraint motion. The motion of mass M is constraint with the motion of P and Q. Let AN = x, NO = z. Then velocity of mass is
From ΔANO, using pythagorous theorem
∴ x2 + z2 = ℓ2
Here x is a constant
Differentiating the above
equation w.r.t to t
A reference frame attached to the earth
Since earth is an accelerated frame and hence, cannot be an inertial frame.
Note : Strictly speaking Earth is accelerated reference frame. Earth is treated as a reference frame for practical examples and Newton's laws are applicable to it only as a limiting case.
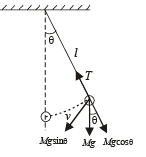
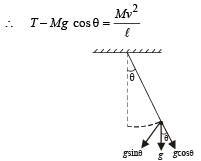
A simple pen dulum of length L an d mass (bob) M is oscillating in a plane about a vertical line between angular limit – φ and + φ . For an angular displacement θ (|θ| < φ), the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions :
Since the body is moving in a circular path therefore it needs centripetal force 
Also, the tangential acceleration acting on the mass is g sin θ.
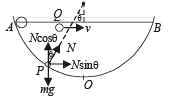
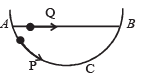
A particle P is sliding down a frictionless hemispherical bowl.
It passes the point A at t = 0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t = 0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then :
At A the horizontal speeds of both the masses is the same. The velocity of Q remains the same in horizontal as no force is acting in the horizontal direction. But in case of P as shown at any intermediate position, the horizontal velocity first increases (due to N sin θ), reaches a max value at O and then decreases. Thus it always remains greater than v. Therefore tP < tQ.
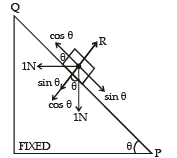
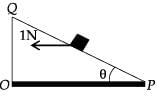
A small block of mass of 0.1 kg lies on a fixed inclined plane PQ which makes an angle θ with the horizontal. A horizontal force of 1 N acts on the block through its centre of mass as shown in the figure.
The block remains stationary if (take g = 10 m/s2)
The forces are resolved as shown in the figure.
When θ = 45º, sinθ = cosθ
The block will remain stationary and the frictional force is zero.
When θ > 45º, sinθ > cosθ
Therefore a frictional force acts towards Q.
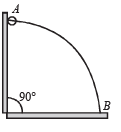
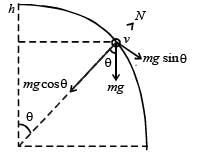
A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
As the bead is moving in the circular path
By energy conservation, 
From (1) and (2)
[N = mg cos θ - m [2g - 2g cosθ]
N = mg cos θ - 2mg + 2mg cosθ
N = 3mg cos θ-2mg
⇒ N = mg (3 cos θ-2)
Clearly N is positive (acts radially outwards) when 
Similarly, N acts radially inwards if 
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Recommended Content
 |
|
 |
|
 |
|
 |
|
 |
|
Recommended Tests
 |
|
|
|
|
|
|
|
|
|
Download free EduRev App
Similar Content
 |
|
|
 |
|
|
|
Related tests
|
|
|
|
|
|
|
|
|
|
|
© EduRev
|
Follow Us
|