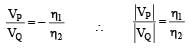Test: MCQs (One or More Correct Option): Mechanical Properties of Solids and Fluids | JEE Advanced - JEE MCQ
9 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Mechanical Properties of Solids and Fluids | JEE Advanced
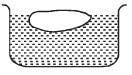
A body floats in a liquid contained in a beaker. The whole system as shown in Figure falls freely under gravity. The upthrust on the body is

The spring balance A reads 2 kg with a block m suspended from it. A balance B reads 5 kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging mass is inside the liquid in the beaker as shown in the figure. In this situation:


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
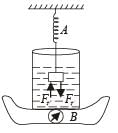
A vessel contains oil (density = 0.8 gm/cm3) over mercury (density = 13.6 gm cm3). A homogeneous sphere floats with half its volume immersed in mercury and the other half in oil.
The density of the material of the sphere in gm/cm3 is
The density of the material of the sphere in gm/cm3 is
Two rods of different materials having coefficients of thermal expansion α1, α2 and Young’s modulii Y1, Y2 respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of the rods. If α1 : α2 = 2 : 3, the thermal stresses developed in the two rods are equal provided Y1 : Y2 is equal to
Water from a tap emerges vertically downwards with an initial spped of 1.0 m s–1. The cross-sectional area of the tap is 10–4 m2. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The crosssectional area of the stream 0.15 m below the tap is
A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statement(s) is (are)
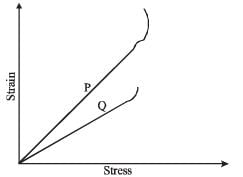
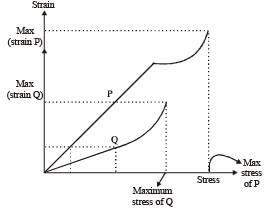
In plotting stress versus strain curves for two materials P and Q,a student by mistake puts strain on the y-axis and stress on the x-axis as shown in the figure. Then the correct statement(s) is (are)
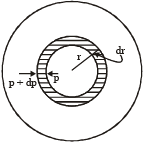
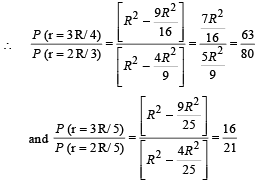
A spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r) is the pressure at r(r < R), then the correct option(s) is (are)
Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut (see figure). If sphere P alone in L2 has terminal velocity 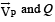 alone in L1 has terminal velocity
alone in L1 has terminal velocity 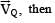

|
347 docs|185 tests
|
|
347 docs|185 tests
|


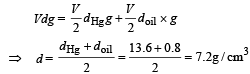
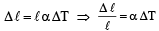
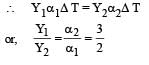
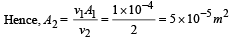


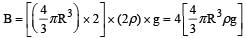
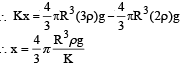
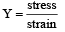
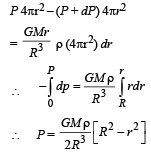
 is negative as ρ1 < σ2
is negative as ρ1 < σ2 is positive as ρ2 > σ1
is positive as ρ2 > σ1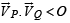 option (d) is correct
option (d) is correct
 ...(i)
...(i)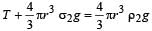 ...(ii)
...(ii)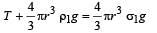 ...(iii)
...(iii)