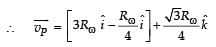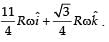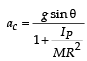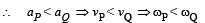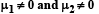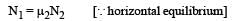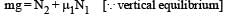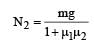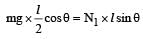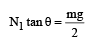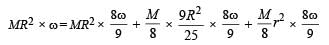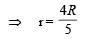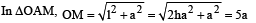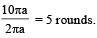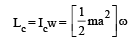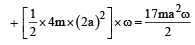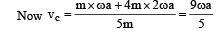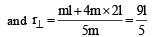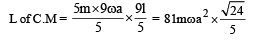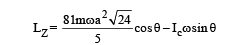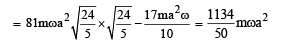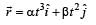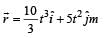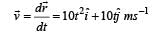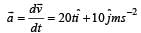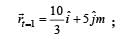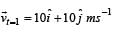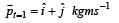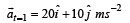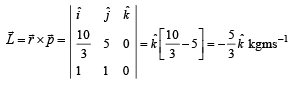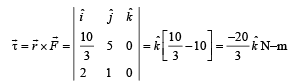Test: MCQs (One or More Correct Option): Rotational Motion | JEE Advanced - JEE MCQ
21 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Rotational Motion | JEE Advanced
Two particles A and B initially at rest, move towards each other under mutual force of attraction. At the instant when the speed of A is V and the speed of B is 2V, the speed of the centre of mass of the system is
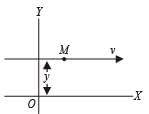
A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
When a bicycle is in motion, the force of friction exerted by the ground on the two wheels is such that it acts
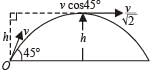
A particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection when the particle is at its maximum height h is
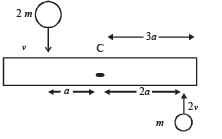
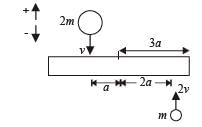
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by w, E and vc respectively, we have after collision
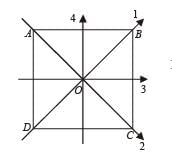
The moment of inertia of a thin square plate ABCD, Fig., of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
wh ere I1, I 2 , I3 andI4 are respectively the momen ts of intertial about axis 1, 2, 3 and 4 which are in the plane of the plate.
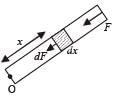
A tube of length L is filled completely with an incomressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is
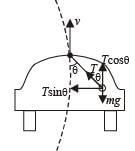
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A pendulum bob is suspended from the roof of the car by a light rigid rod of length 1.00 m. The angle made by the rod with track is
Let I be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle q with AB. The moment of inertia of the plate about the axis CD is then equal to
The torqueτ on a body about a given point is found to be equal to A × L where A is a constant vector, and L is the angular momentum of the body about that point. From this it follows that
A solid cylinder is rolling down a rough inclined plane of inclination θ. Then
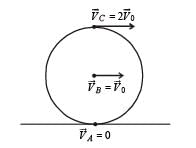
If the resultant of all the external forces acting on a system of particles is zero, then from an inertial frame, one can surely say that
A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then,
Two solid spheres A and B of equal volumes but of different densities dAand dBare connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
A thin ring of mass 2 kg and radius 0.5 m is rolling without on a horizontal plane with velocity 1 m/s. A small ball of mass 0.1 kg, moving with velocity 20 m/s in the opposite direction hits the ring at a height of 0.75 m and goes vertically up with velocity 10 m/ s. Immediately after the collision
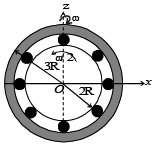
The figure shows a system consisting of (i) a ring of outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti-clockwise with angular speed ω/2. The ring and disc are separated by frictionless ball bearings. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30° with the horizontal. Then with respect to the horizontal surface,
Two solid cylinders P and Q of same mass and same radius start rolling down a fixed inclined plane from the same height at the same time. Cylinder P has most of its mass concentrated near its surface, while Q has most of its mass concentrated near the axis. Which statement(s) is(are) correct?
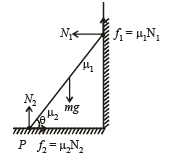
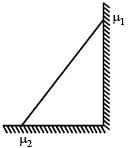
In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angleθ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. The normal reaction of the wall on the ladder is N1 and that of the floor is N2. If the ladder is about to slip, then
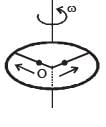
A ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M/8 at rest at O. Thesemasses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 8/9 ω and one of the masses is
at a distance of 3/5 R from O. At this instant the distance of the other mass from O is
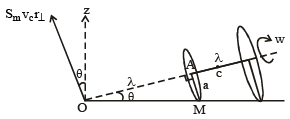
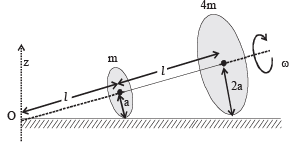
Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length 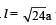 through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momentum of the entire assembly about the point
through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momentum of the entire assembly about the point (see the figure)Which of the following statement(s) is (are) true?
The position of a particle of mass m is given by the following equation
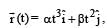
where 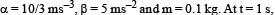 which of the following statement(s) is(are) true about the particle?
which of the following statement(s) is(are) true about the particle?
|
347 docs|185 tests
|
|
347 docs|185 tests
|


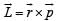

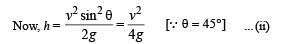
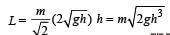
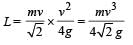
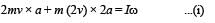
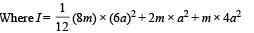
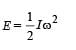
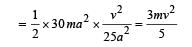
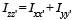
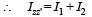
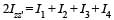
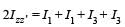
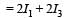
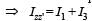
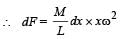
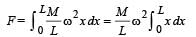
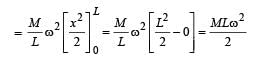
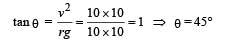
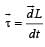
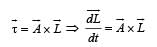
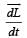 uur is always perpendicular to the
uur is always perpendicular to the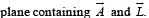
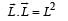
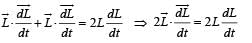
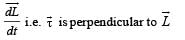
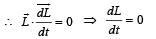
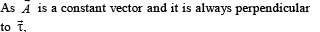
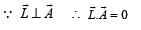
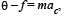

 From (i) and (ii)
From (i) and (ii) 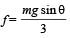
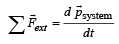
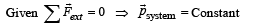
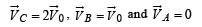
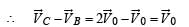
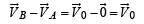
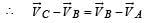
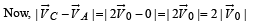
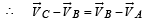
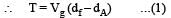
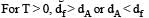
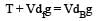
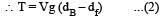
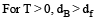
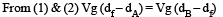
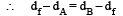
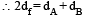

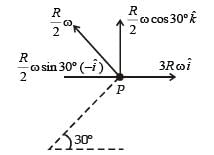
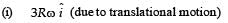
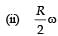 making an angle of 30º with the vertical due to rotation
making an angle of 30º with the vertical due to rotation