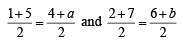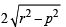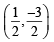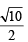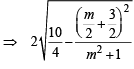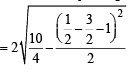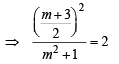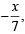Test: MCQs (One or More Correct Option): Straight Lines and Pair of Straight Lines | JEE Advanced - JEE MCQ
9 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Straight Lines and Pair of Straight Lines | JEE Advanced
Three lines px + qy + r = 0, qx + ry + p = 0 and rx + py + q = 0 are concurrent if (1985 - 2 Marks)
The points  (1, 3) and (82, 30) are vertices of
(1, 3) and (82, 30) are vertices of
 (1, 3) and (82, 30) are vertices of
(1, 3) and (82, 30) are vertices of| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
All points lying inside the triangle formed by the points (1, 3), (5, 0) and (–1, 2) satisfy (1986 - 2 Marks)
A vector 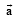 has components 2p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If, with respect to the new system , ar has components p + 1 and 1, then (1986 - 2 Marks)
has components 2p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If, with respect to the new system , ar has components p + 1 and 1, then (1986 - 2 Marks)
If (P(1, 2), Q(4, 6), R(5, 7) and S(a, b) are the vertices of a parallelogram PQRS, then (1998 - 2 Marks)
The diagonals of a parallelogram PQRS are along the lines x +3y = 4 and 6x – 2y = 7. Then PQRS must be a. (1998 - 2 Marks)
If the vertices P, Q, R of a triangle PQR are rational points, which of the following points of the triangle PQR is (are) always rational point(s)? (1998 - 2 Marks)
Let L1 be a strainght line passing through the origin and L2 be the straight line x +y = 1. If the intercepts made by the circle x2 + y2 - x + 3y= 0 on L1 and L2 are equal, then which of the following equations can represent L1? (1999 - 3 Marks)
For a > b > c > 0, the distance between (1, 1) and the point of intersection of the lines ax + by + c = 0 and bx + ay + c = 0 is less than 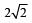 . Then (JEE Adv. 2013)
. Then (JEE Adv. 2013)
|
347 docs|185 tests
|
|
347 docs|185 tests
|


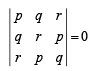
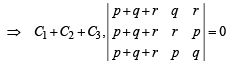


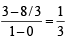
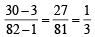
 with respect to original axes and a = ( p + 1) i+j with respect to new axes.
with respect to original axes and a = ( p + 1) i+j with respect to new axes.