Test: Mathematical Physics - 1 - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2025 - Test: Mathematical Physics - 1
The particular integral of (4D2 + 4D + 1) y = 8e-x/2 is
The vector [1, 2, 3], [1, 0, 0], [0, 1, 0], [0, 0, 1] are
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Real part of the 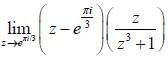 is ______ (upto two decimal places)
is ______ (upto two decimal places)
Given z3 = 1. Let z0,z1 and z2 be the complex roots of the above equation.If z0 = 1, then the value of z1z2 is ____ (Answer should be an integer)
The dimensionality of the vector space of hermitian 3 x 3 matrices is ____ (answer should be an integer)
Given vector  the line integral
the line integral 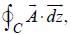 where C is a circle of radius 5 units with its center at origin is ________
where C is a circle of radius 5 units with its center at origin is ________
The determinant of the metric tensor corresponding to ds2 = 5(dx1)2 + 3(dx2)2 + 4(dx3)2 - 6dx1dx2 + 4dx2dx3 is
Consider a vector v = (v1, v2, v3) in three dimensional complex vector space c3. A linear operator T is designed as follows
T( v1, v2, v3) = ( v1, v2 - v3,iv2)
Find T+ matrix representation using orthonormal basis
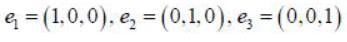
Given the Legendre polynomial P0(x) = 1, P1 (x) = x and 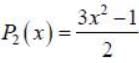 then polynomial (3x2 + x -1)
then polynomial (3x2 + x -1)
Find the complex coefficient Cn of the fourier series of the function 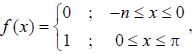 for n is odd.
for n is odd.
The equation of the plane that is tangent to the surface xyz = 8 at point (1,2,4) is
The value of the integral 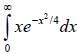 is ______ (upto two decimal places)
is ______ (upto two decimal places)
The value of the Contour integral
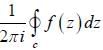
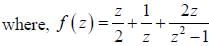
and the contour C is a circle of radius 2 centred at the origin traversed in the counterclockwise direction is ______ (answer should be an integer).
|
1 docs|34 tests
|


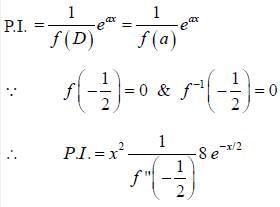
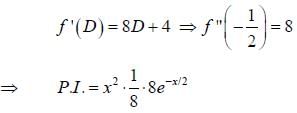
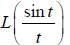
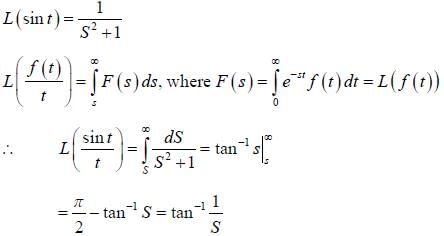
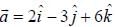 on vector
on vector 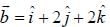
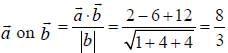

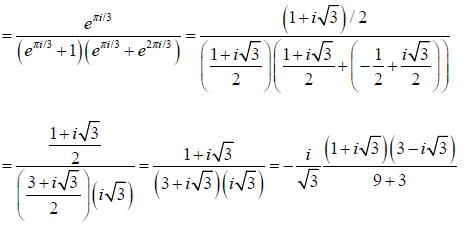
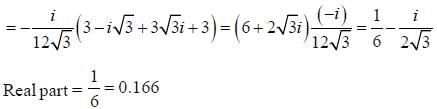
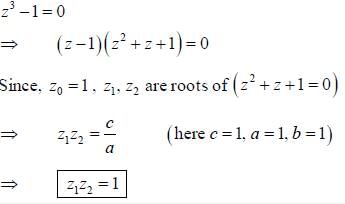
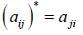
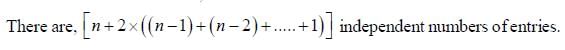
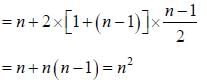
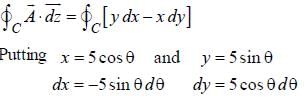
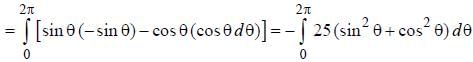
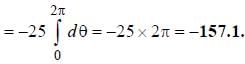
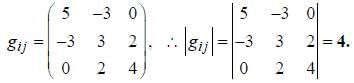
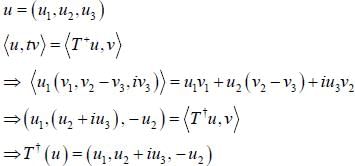

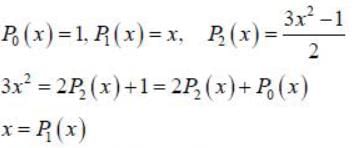
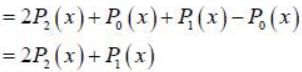
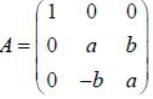 is orthogonal if
is orthogonal if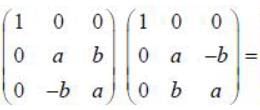
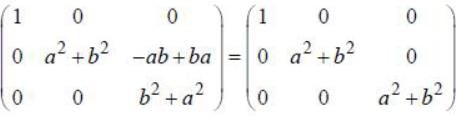

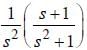
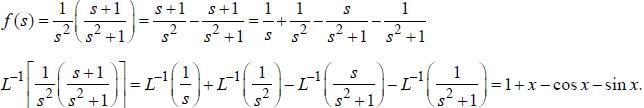
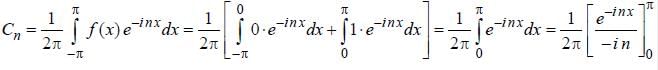
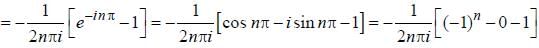
 is normal to surface
is normal to surface 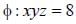 at point P(1,2,4). Therefore,
at point P(1,2,4). Therefore, 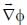 is perpendicular to vector
is perpendicular to vector 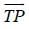 lying in the tangent plane of the given surface.
lying in the tangent plane of the given surface.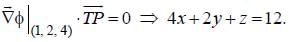
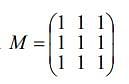
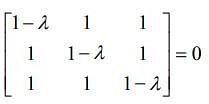
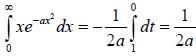
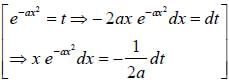
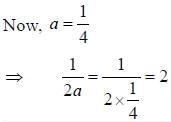
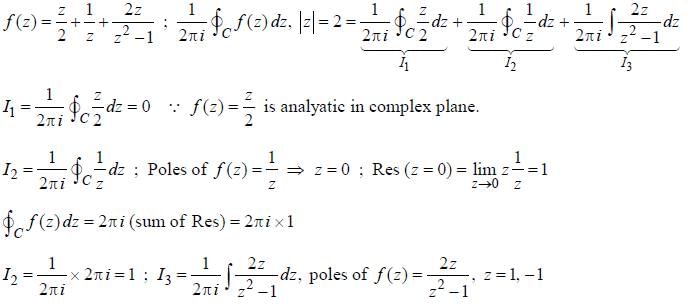
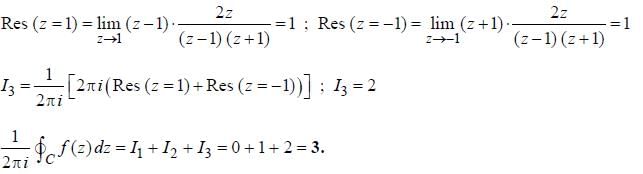
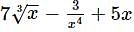 with respect x?
with respect x?
















