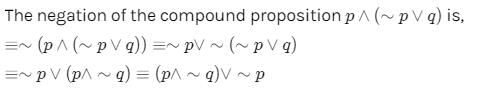Test: Mathematical Reasoning- 2

Let p and q be two propositions. Then the contrapositive of the implication p→q is

Let p and q be two propositions. Then the implication ∼(p↔q)∼(p↔q) is :

p∧(q∧r) is logically equivalent to

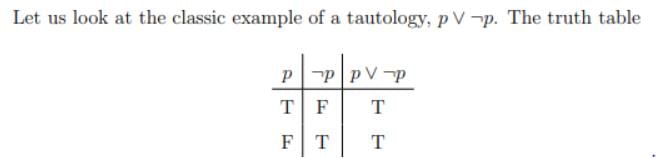
Which of the following proposition is a tautology ?

The negation of the compound statement p∨(∼p∨q) is

The proposition p→∼(p∧∼q) is

The proposition (p→∼p)∧(∼p→p) is

Which of the following is equivalent to (p∧q) ?

Which of the following is logically equivalent to ∼(∼p→q) ?

The contrapositive of the inverse of p⇒ ~q is

p→q is logically equivalent to

The contrapositive of (∼p∧q)→ is

The negation of p∧∼(q∧r) is

The negation of q∨∼(p∧r) is

Which of the following is a contradiction?

Which of the following is logically equivalent to (p∧q) ?

The negation of the proposition q∨∼(p∧r) is

If p→(q∨r) is false , then the truth values of p , q and r, are respectively

The statement p ⇒ p∨q is

The statement p∨qp∨q is

Which of the following sentences is a statement ?

Let p and q be two prepositions given by p : I take only bread and butter in breakfast. q : I do not take anything in breakfast. Then , the compound proposition “ I take only bread and butter in breakfast or I do not take anything “ is represented by