Test: Moment Of Inertia For Areas - Mechanical Engineering MCQ
15 Questions MCQ Test Additional Study Material for Mechanical Engineering - Test: Moment Of Inertia For Areas
Whenever the distributed loading acts perpendicular to an area its intensity varies __________
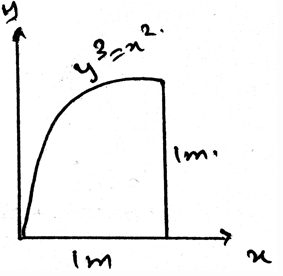
Determine the moment of inertia of the area about y-axis.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The calculation of the moment of the body due to the loadings involve a quantity called ____________
Moment of Inertia is the integration of the square of the distance of the centroid and the del area along the whole area of the structure.
There is perpendicular axis theorem for the area.
What is parallel axis theorem and to whom it is applied?
The parallel axis theorem gives the moment of inertia ______________ to the surface of considerance.
The parallel axis theorem can add any angle varied moment of inertias to give the perpendicular moment of inertia.
The parallel axis theorem uses the ____________ of the distance.
The distance in the parallel axis theorem is multiplied by ___________
One of the use of the centre of mass or centroid is as in the moment of inertia is that the net force acts at the ___________ of the loading body.
If the non-Uniform loading is of the type of parabola then for calculating the moment of inertia for areas?
If any external force also is applied on the structure and we are determining the moment of inertia then what should we consider?
The body is sometimes acted by two or three force members and we need to find the moment of inertia for the same. The difference between the two and the three force members is:
Determine the moment of inertia of the area about x-axis.
|
1 videos|30 docs|57 tests
|
|
1 videos|30 docs|57 tests
|

















