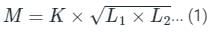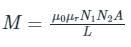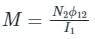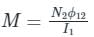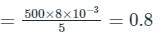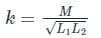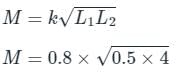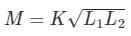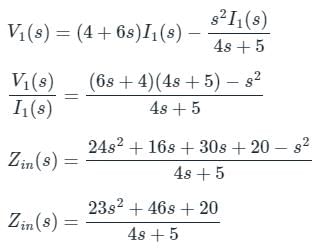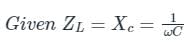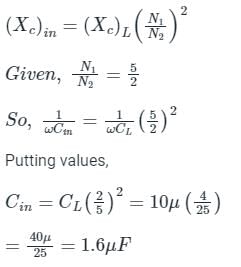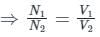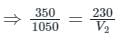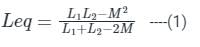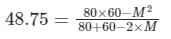Test: Mutual Inductance - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Mutual Inductance - 1
A 5 H coil is coupled with a 20 H coil. What could be the maximum value of mutual inductance between them considering no flux linkage?
Identify the INCORRECT statement among the given options regarding mutual inductance.
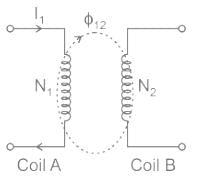
What is the basic operating principle of mutual induction?
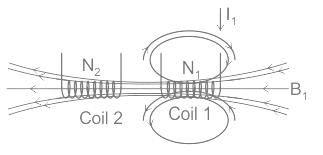
Two identical coils X and Y of 500 turns each lie in parallel planes such that 80% of flux produced by one coil links with the other. If a current of 5 A flowing in X produces a flux of 10 mWb in it, find the mutual inductance between X and Y
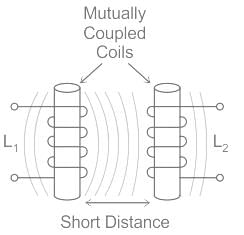
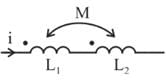
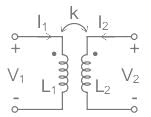
Two coupled coils with L1 = 0.5 H and L2 = 4.0 H have a co-efficient of coupling 0.8. Find maximum value of the inductance EMF in the coil 2 if a current of i1 = 20 sin 314t A is passed in coil 1.
Two inductors L1 = 20 mH and L2 = 40 mH are connected in series so that their equivalent inductance is 50 mH. The mutual inductance between the two coils is _______.
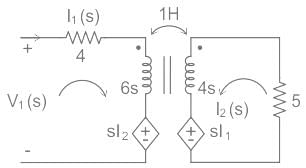
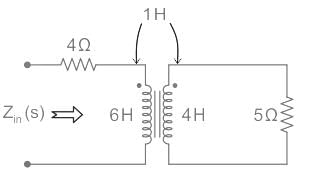
The input impedance, Zin (s), for the network shown is
10 μF capacitor is connected across the secondary winding of a high-frequency transformer having primary to secondary turns ratio 5: 2. What is the value of capacitance seen across primary?
A transformer has 350 primary turns and 1050 secondary turns. The primary winding is connected across a 230 V, 50 Hz supply. The induced EMF in the secondary will be
Two inductors whose self-inductance is 80 mH and 60 mH are connected in parallel aiding. The equivalent inductance of the combination is 48.75 mH. Calculate their mutual inductance.