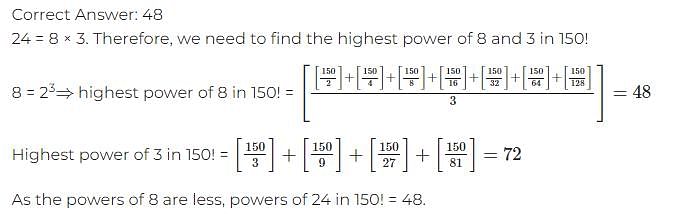Test: Number System (January 9) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Number System (January 9)
Rohan purchased some pens, pencils and erasers for his young brothers and sisters for the ensuing examinations. He had to buy atleast 11 pieces of each item in a manner that the number of pens purchased is more than the number of pencils, which is more than the number of erasers. He purchased a total of 38 pieces. If the number of pencils cannot be equally divided among his 4 brothers and sisters, how many pens did he purchase?
A nursery has 363, 429 and 693 plants respectively of 3 distinct varieties. It is desired to place these plants in straight rows of plants of 1 variety only so that the number of rows required is the minimum. What is the size of each row and how many rows would be required?
1 ’s are given 100 times, 2 ’s are given 100 times and 3’s are given 100 times. Now numbers are made by arranging these 300 digits in all possible ways. How many of these numbers will be perfect squares?
Find the remainder when 73 * 75 * 78 * 57 * 197 * 37 is divided by 34.
Four bells ring together and ring at an interval of 12 sec, 15 sec, 20 sec, and 30 sec respectively. How many times will they ring together in 8 hours?
After the division of a number successively by 3, 4 and 7, the remainders obtained are 2, 1 and 4 respectively. What will be the remainder if 84 divides the same number?
Teacher said that there were 100 students in his class, 24 of whom were boys and 32 were girls. Which base system did the teacher use in this statement?
If a three digit number ‘abc’ has 2 factors (where a, b, c are digits), how many factors does the 6-digit number ‘abcabc’ have?
|
152 docs|327 tests
|