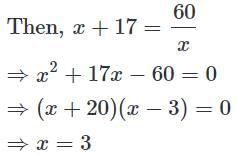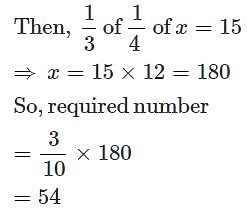All Courses
Get the App Signup / Login
Sign in Open App
Class 8 Exam  >  Class 8 Tests  >  Know Your Aptitude Class 6 To 8  >  Test: Numbers - Class 8 MCQ

Test: Numbers - Class 8 MCQ


Test Description

10 Questions MCQ Test Know Your Aptitude Class 6 To 8 - Test: Numbers

Test: Numbers for Class 8 2024 is part of Know Your Aptitude Class 6 To 8 preparation. The Test: Numbers questions and answers have been prepared according to the Class 8 exam syllabus.The Test: Numbers MCQs are made for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Numbers below.
Solutions of Test: Numbers questions in English are available as part of our Know Your Aptitude Class 6 To 8 for Class 8 & Test: Numbers solutions in Hindi for Know Your Aptitude Class 6 To 8 course. Download more important topics, notes, lectures and mock test series for Class 8 Exam by signing up for free. Attempt Test: Numbers | 10 questions in 15 minutes | Mock test for Class 8 preparation | Free important questions MCQ to study Know Your Aptitude Class 6 To 8 for Class 8 Exam | Download free PDF with solutions
Test: Numbers - Question 1
Save

Find a positive number which when increased by 17 is equal to 60 times the reciprocal of the number.

Detailed Solution for Test: Numbers - Question 1

Let the number be x

Test: Numbers - Question 2
Save

In a two-digit, if it is known that its unit's digit exceeds its ten's digit by 2 and that the product of the given number and the sum of its digits is equal to 144, then the number is:

Detailed Solution for Test: Numbers - Question 2

Let the ten's digit be x
Then, unit's digit = x + 2
Number = 10x + (x + 2) = 11x + 2
Sum of digits = x + (x + 2) = 2x + 2
∴ (11x + 2)(2x + 2) = 144
⇒ 22x2 + 26x - 140 = 0
⇒ 11x2 + 13x - 70 = 0
⇒ 11x2 + (35 - 22)x - 70 = 0
⇒ 11x2 + 35x - 22x - 70 = 0
⇒ (x - 2)(11x + 35) = 0
⇒ x = 2
Hence, required number = 11x + 2 = 24

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Numbers - Question 3
Save

A number consists of two digits. If the digits interchange places and the new number is added to the original number, then the resulting number will be divisible by:

Detailed Solution for Test: Numbers - Question 3

Let the ten's digit be x and unit's digit be y.
Then, number = 10x + y
Number obtained by interchanging the digits = 10y + x
∴ (10x + y) + (10y + x) = 11(x + y), which is divisible by 11

Test: Numbers - Question 4
Save

The sum of the squares of three numbers is 138, while the sum of their products taken two at a time is 131. Their sum is:
Detailed Solution for Test: Numbers - Question 4

Let the numbers be a, b and c
Then, a2 + b2 + c2 = 138 and (ab + bc + ca) = 131
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca) = 138 + 2 x 131 = 400
⇒ (a + b + c) = √400 = 20

Test: Numbers - Question 5
Save

The sum of the digits of a two-digit number is 15 and the difference between the digits is 3. What is the two-digit number?
Detailed Solution for Test: Numbers - Question 5

Let the ten's digit be x and unit's digit be y
Then, x + y = 15 and x - y = 3   or   y - x = 3
Solving x + y = 15   and   x - y = 3, we get: x = 9, y = 6
Solving x + y = 15   and   y - x = 3, we get: x = 6, y = 9
So, the number is either 96 or 69
Hence, the number cannot be determined.

Test: Numbers - Question 6
Save

A two-digit number is such that the product of the digits is 8. When 18 is added to the number, then the digits are reversed. The number is:
Detailed Solution for Test: Numbers - Question 6

Let the ten's and unit digit be x and 8/x respectively
Then,

∴ first digit will be 2 and second digit will be 4.
i.e digit is 24.

Test: Numbers - Question 7
Save

The difference between a two-digit number and the number obtained by interchanging the digits is 36. What is the difference between the sum and the difference of the digits of the number if the ratio between the digits of the number is 1 : 2?
Detailed Solution for Test: Numbers - Question 7

Since the number is greater than the number obtained on reversing the digits, so the ten's digit is greater than the unit's digit.
Let ten's and unit's digits be 2x and x respectively.
Then, (10 × 2x + x) - (10x + 2x) = 36
⇒ 9x = 36
⇒ x = 4
∴ Required difference
= (2x + x) - (2x - x)
= 2x
= 8

Test: Numbers - Question 8
Save

The difference between a two-digit number and the number obtained by interchanging the positions of its digits is 36. What is the difference between the two digits of that number?
Detailed Solution for Test: Numbers - Question 8

Let the ten's digit be x and unit's digit be y.
Then, (10x + y) - (10y + x) = 36
⇒ 9(x - y) = 36
⇒ x - y = 4

Test: Numbers - Question 9
Save

Three times the first of three consecutive odd integers is 3 more than twice the third. The third integer is:
Detailed Solution for Test: Numbers - Question 9

Let the three integers be x, x + 2 and x + 4
Then, 3x = 2(x + 4) + 3 ⇔ x = 11
∴ Third integer = x + 4 = 15

Test: Numbers - Question 10
Save

If one-third of one-fourth of a number is 15, then three-tenth of that number is:
Detailed Solution for Test: Numbers - Question 10

Let the number be x 

5 videos|60 docs|13 tests
Join Course
Information about Test: Numbers Page
In this test you can find the Exam questions for Test: Numbers solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Numbers, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 8

Download as PDF

Top Courses for Class 8

Important Questions for Numbers

Find all the important questions for Numbers at EduRev.Get fully prepared for Numbers with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Numbers syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Numbers resources.

Numbers MCQs with Answers

Prepare for the Numbers within the Class 8 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Numbers Know Your Aptitude Class 6 To 8

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Numbers with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup