Test: Overlapping SETS- 2 - GMAT MCQ
10 Questions MCQ Test - Test: Overlapping SETS- 2
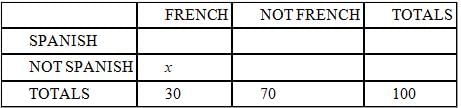
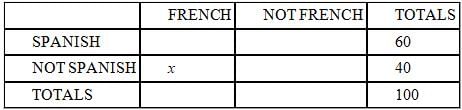
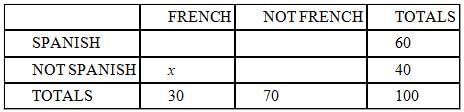
What percent of the students at Jefferson High School study French but not Spanish?
(1) 30% of all students at Jefferson High School study French.
(2) 40% of all students at Jefferson High School do not study Spanish.
(1) 30% of all students at Jefferson High School study French.
(2) 40% of all students at Jefferson High School do not study Spanish.
If none of the students are ambidextrous, what percentage of the 20 students in Mr. Henderson's class are
left-handed?
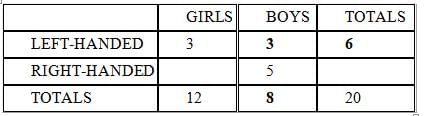
(1) Of the 12 girls in the class, 25% are left-handed.
(2) 5 of the boys in the class are right-handed.
left-handed?
(1) Of the 12 girls in the class, 25% are left-handed.
(2) 5 of the boys in the class are right-handed.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
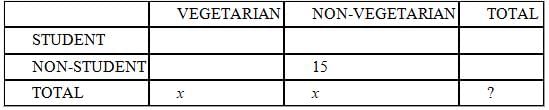
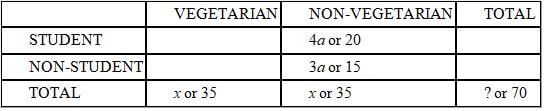
Guests at a recent party ate a total of fifteen hamburgers. Each guest who was neither a student nor a
vegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, a
vegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?
(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate for
non-vegetarians.
(2) 30% of the guests were vegetarian non-students.
vegetarian ate exactly one hamburger. No hamburger was eaten by any guest who was a student, a
vegetarian, or both. If half of the guests were vegetarians, how many guests attended the party?
(1) The vegetarians attended the party at a rate of 2 students to every 3 non-students, half the rate for
non-vegetarians.
(2) 30% of the guests were vegetarian non-students.
To receive a driver license, sixteen year-olds at Culliver High School have to pass both a written and a
practical driving test. Everyone has to take the tests, and no one failed both tests. If 30% of the 16 year-olds who passed the written test did not pass the practical, how many sixteen-year-olds at Culliver High School
received their driver license?
(1) There are 188 sixteen year-olds at Culliver High School.
(2) 20% of the sixteen year-olds who passed the practical test failed the written test.
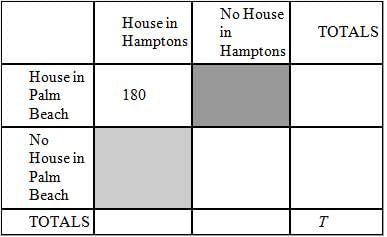
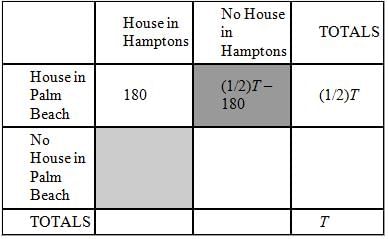
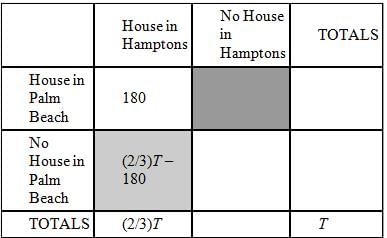
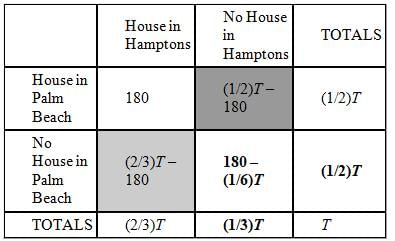
At a charity fundraiser, 180 of the guests had a house both in the Hamptons and in Palm Beach. If not
everyone at the fundraiser had a house in either the Hamptons or Palm Beach, what is the ratio of the
number of people who had a house in Palm Beach but not in the Hamptons to the number of people who had
a house in the Hamptons but not in Palm Beach?
(1) One-half of the guests had a house in Palm Beach.
(2) Two-thirds of the guests had a house in the Hamptons
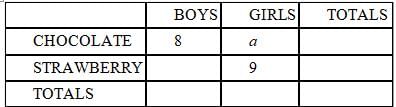
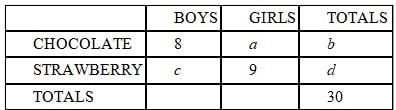
Recently Mary gave a birthday party for her daughter at which she served both chocolate and strawberry ice
cream. There were 8 boys who had chocolate ice cream, and nine girls who had strawberry. Everybody there
had some ice cream, but nobody tried both. What is the maximum possible number of girls who had some
chocolate ice cream?
Exactly thirty children attended the party.
Fewer than half the children had strawberry ice cream.
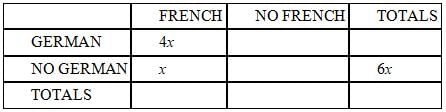
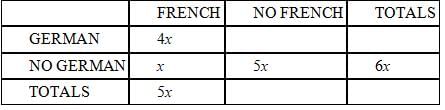
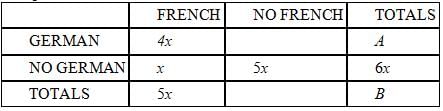
Many of the students at the International School speak French or German or both. Among the students who
speak French, four times as many speak German as don't. In addition, 1/6 of the students who don't speak
German do speak French. What fraction of the students speak German?
(1) Exactly 60 students speak French and German.
(2) Exactly 75 students speak neither French nor German.
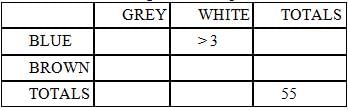
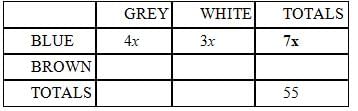
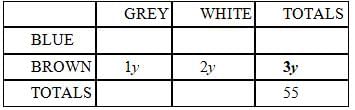
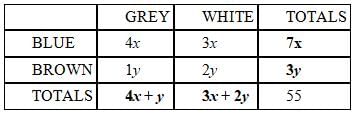
Each member of a pack of 55 wolves has either brown or blue eyes and either a white or a grey coat. If there
are more than 3 blue-eyed wolves with white coats, are there more blue-eyed wolves than brown-eyed
wolves?
(1) Among the blue-eyed wolves, the ratio of grey coats to white coats is 4 to 3.
(2) Among the brown-eyed wolves, the ratio of white coats to grey coats is 2 to 1.
What percentage of the current fourth graders at Liberation Elementary School dressed in costume for
Halloween for the past two years in a row (both this year and last year)?
(1) 60% of the current fourth graders at Liberation Elementary School dressed in costume for Halloween this
year.
(2) Of the current fourth graders at Liberation Elementary School who did not dress in costume for
Halloween this year, 80% did not dress in costume last year.
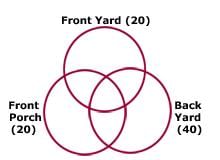
Of all the houses on Kermit Lane, 20 have front porches, 20 have front yards, and 40 have back yards. How
many houses are on Kermit Lane?
(1) No house on Kermit Lane is without a back yard.
(2) Each house on Kermit Lane that has a front porch does not have a front yard.


 The correct answer is E.
The correct answer is E.
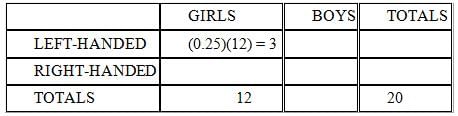





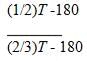
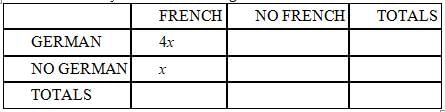
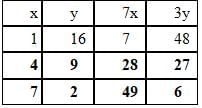
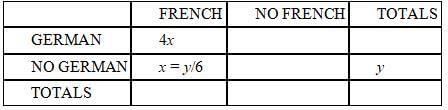 Now since x = y/6, we can get rid of the new variable y and keep all the expressions in terms of x.
Now since x = y/6, we can get rid of the new variable y and keep all the expressions in terms of x.