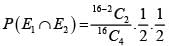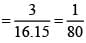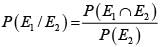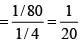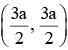Test: Parabola (20 July) - JEE MCQ
15 Questions MCQ Test Daily Test for JEE Preparation - Test: Parabola (20 July)
The equation of parabola whose focus is (– 3, 0) and directrix x + 5 = 0 is:
A parabola whose axis is along the y-axis, vertex is (0,0) and point from the first and second quadrants lie on it, has the equation of the type
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The equation y2 + 3 = 2(2x+y) represents a parabola with the vertex at
The equation of the parabola with vertex at (0, 0) and focus at (0, – 2) is:
The …… of a conic is the chord passing through the focus and perpendicular to the axis.
If the line x + y – 1 = 0 touches the parabola y2 = kx , then the value of k is
Directrix of a parabola is x + y = 2. If it's focus is origin, then latus rectum of the parabola is equal to
Which one of the following equations represents parametrically, parabolic profile ?
If (t2, 2t) is one end of a focal chord of the parabola y2 = 4x then the length of the focal chord will be
From the focus of the parabola y2 = 8x as centre, a circle is described so that a common chord of the curves is equidistant from the vertex and focus of the parabola. The equation of the circle is
In a knockout tournament 16 equally skilled players namely P1, P2, -------- P16 are participating. In each round players are divided in pairs at random and winner from each pair moves in the next round. If P2 reaches the semifinal, then the probability that P1 will win the tournament is.
If the parametric equations of the parabola are given by x = 4t2 - 2t + 1; y = 3t2 + t + 1 and the vertex of the parabola also satisfies y - x = k/100, then the area of the circle x2 + y2 + 12x -10y + 2k = 0 in square units is
A parabola has focus at (0, 0) and passes through the points (4, 3) and (–4, –3). The number of lattice points (x, y) on the parabola such that |4x + 3y| < 1000 is
Center of the smallest circle that is drawn to touch the two parabolas given by y2 + 2x + 2y + 3 = 0; x2 + 2x + 2y + 3 = 0 is
The equation of directrix and latusrectum of a parabola are 3x – 4y + 27 = 0 and 3x – 4y + 2 = 0. Then the length of latusrectum is
|
360 tests
|