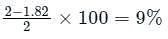Test: Percentages - 1 - SAT MCQ
10 Questions MCQ Test Mathematics for Digital SAT - Test: Percentages - 1
The price of wheat is reduced by 4%. How many more or less kg of wheat can now be bought for the money which was sufficient to buy 48 kg wheat earlier?
The difference between the 30% of a number and 22% of that number is 4800. What is the 18% of that number?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
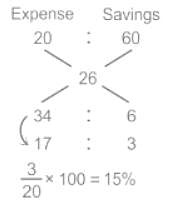
Kamal saves x% of her monthly income. When her monthly expenditure is increased by 20% and the monthly income is increased by 26%, then her monthly savings increased by 60%. What is the value of x?
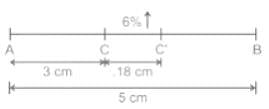
A and B are two fixed points 5 cm apart and C is a point on AB such that AC is 3 cm. If the Length of AC is increased by 6%, the length of CB is decreased by how many %?
In an election, there is neck to neck competition between two candidates A and B. Candidate A got 54% of valid votes and won by 3200 votes. If 20% of the votes cast in the election are invalid. Then find the total votes cast in the election.
800 g of sugar solution has 40% sugar in it. How much sugar should be added to make its proportion at 60% in the solution?
The difference between the 41% of a number and 33% of that number is 960. Then, what is the value of 33.33% of that number?
The price of sugar is increased by 25%. If a family wants to keep its expenses on sugar unaltered, then the familiy will have to reduce the consumption of sugar by:
A student got 20% marks and failed by 72 marks. If he scores 40% marks then he gets 8 marks more than the passing marks. Find the passing marks.
Two numbers are 50% and 75% lesser than a third number. By how much percent is the second number to be enhanced to make it equal to the first number?
|
185 videos|124 docs|75 tests
|
|
185 videos|124 docs|75 tests
|