Test: Permutation & Combination- 3 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Permutation & Combination- 3
A gambler began playing blackjack with $110 in chips. After exactly 12 hands, he left the table with $320 in chips, aving won some hands and lost others. Each win earned $100 and each loss cost $10. How many possible utcomes were there for the first 5 hands he played? (For example, won the first hand, lost the second, etc.)
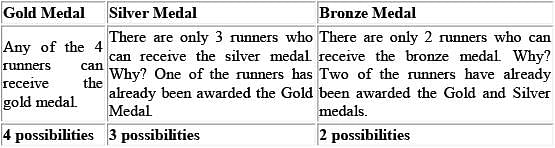
In a 4 person race, medals are awarded to the fastest 3 runners. The first-place runner receives a gold medal, the second-place runner receives a silver medal, and the third-place runner receives a bronze medal. In the event of a tie, the tied runners receive the same color medal. (For example, if there is a two-way tie for firstplace, the top two runners receive gold medals, the next-fastest runner receives a silver medal, and no bronze medal is awarded). Assuming that exactly three medals are awarded, and that the three medal winners stand together with their medals to form a victory circle, how many different victory circles are possible?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The organizers of a week-l ong fair have hired exactly five security guards to patrol the fairgrounds at night for the duration of the event. Exactly two guards are assigned to patrol the grounds every night, with no guard assigned consecutive nights. If the fair begins on a Monday, how many different pairs of guards will be available to patrol the fairgrounds on the following Saturday night?
Larry, Michael, and Doug have five donuts to share. If any one of the men can be given any whole number of donuts from 0 to 5, in how many different ways can the donuts be distributed?
A woman has seven cookies—four chocolate chip and three oatmeal. She gives one cookie to each of her six children: Nicole, Ronit, Kim, Deborah, Mark, and Terrance. If Deborah will only eat the kind of cookie that Kim eats, in how many different ways can the cookies be distributed? (The leftover cookie will be given to the dog.)
How many different combinations of outcomes can you make by rolling three standard (6-sided) dice if the order of the dice does not matter?
A certain league has four divisions. The respective divisions had 9, 10, 11, and 12 teams qualify for the playoffs. Each division held its own double-elimination tournament -- where a team is eliminated from the tournament upon losing two games -- in order to determine its champion. The four division champions then played in a single-elimination tournament -- where a team is eliminated upon losing one game -- in order to determine the overall league champion. Assuming that there were no ties and no forfeits, what is the maximum number of games that could have been played in order to determine the overall league champion?
You have a bag of 9 letters: 3 Xs, 3 Ys, and 3 Zs. You are given a box divided into 3 rows and 3 columns for a total of 9 areas. How many different ways can you place one letter into each area such that there are no rows or columns with 2 or more of the same letter?

Eight women of eight different heights are to pose for a photo in two rows of four. Each woman in the second row must stand directly behind a shorter woman in the first row. In addition, all of the women in each row must be arranged in order of increasing height from left to right. Assuming that these restrictions are fully adhered to, in how many different ways can the women pose?
You have a six-sided cube and six cans of paint, each a different color. You may not mix colors of paint. How many distinct ways can you paint the cube using a different color for each side? (If you can reorient a cube to look like another cube, then the two cubes are not distinct.)
A group of four women and three men have tickets for seven adjacent seats in one row of a theatre. If the three men will not sit in three adjacent seats, how many possible different seating arrangements are there for these 7 theatre-goers?
Anthony and Michael sit on the six-member board of directors for company X. If the board is to be split up into 2 three-person subcommittees, what percent of all the possible subcommittees that include Michael also include Anthony?
A family consisting of one mother, one father, two daughters and a son is taking a road trip in a sedan. The sedan has two front seats and three back seats. If one of the parents must drive and the two daughters refuse to sit next to each other, how many possible seating arrangements are there?
Six mobsters have arrived at the theater for the premiere of the film “Goodbuddies.” One of the mobsters, Frankie, is an informer, and he's afraid that another member of his crew, Joey, is on to him. Frankie, wanting to keep Joey in his sights, insists upon standing behind Joey in line at the concession stand. How many ways can the six arrange themselves in line such that Frankie’s requirement is satisfied?
A student committee that must consist of 5 members is to be formed from a pool of 8 candidates. How many different committees are possible?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|


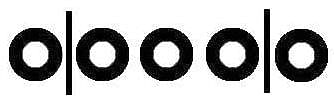

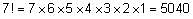
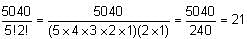

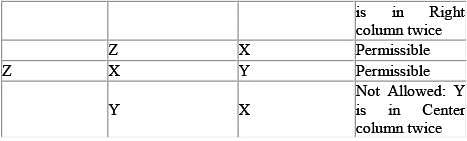
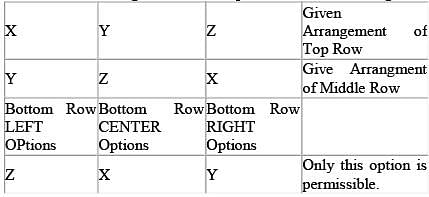
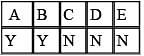
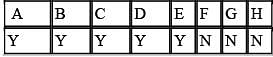 The total number of possible five-person committees that can be created from a group of 8 candidates will be equal to the number of possible anagrams that can be formed from the word YYYYYNNN = 8! / (5!3!) = 56. Therefore, there are a total of 56 possible committees.
The total number of possible five-person committees that can be created from a group of 8 candidates will be equal to the number of possible anagrams that can be formed from the word YYYYYNNN = 8! / (5!3!) = 56. Therefore, there are a total of 56 possible committees.














