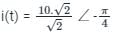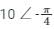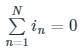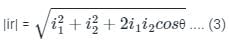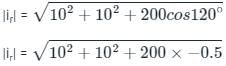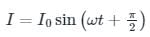Test: Phasor Diagrams - Electrical Engineering (EE) MCQ
15 Questions MCQ Test Network Theory (Electric Circuits) - Test: Phasor Diagrams
The voltage applied to a circuit is 100 √2 cos (100πt) volts and the circuit draws a current of 10 √2 sin (100πt + π / 4) amperes. Taking the voltage as the reference phasor, the phasor representation of the current in amperes is
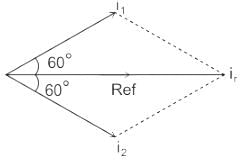
Three currents i1, i2, and i3 meet at a node. if i1 = 10 sin (400t + 60°) A, and i2 = 10sin (400t - 60°) A then i3 =
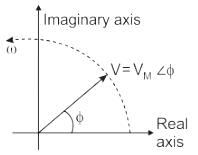
In phasor representation of an alternating quantity, the sinusoidally varying alternating quantity can be represented graphically by:
The current in the inductive circuit is 10 A and power factor is 0.866. The phasor representation of current is:
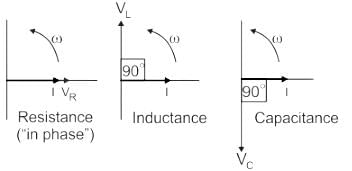
For a pure resistance supplied through a sinusoidal voltage, the phase difference between the voltage and current phasors will be _______.
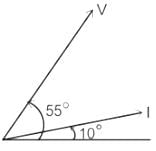
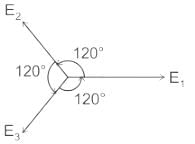
Three different coils produce a same EMF of 100 V when moved at a constant speed in the magnetic field. The induced EMF in the first coil lags to the induced EMF in the second coil and leads to the induced EMF in the third coil. So, what will be the resultant EMF in the series combination of the three coils?
A phasor
1. may be a scalar or a vector
2. is a time-dependent quantity
3. is a complex quantity
Which of the above statements are correct?
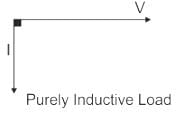
The phase difference between current and voltage in a pure capacitive circuit is:
The non linear magnetization curve of a practical transformer will introduce _________
Which of the following equation correctly represents the exact phasor diagram of transformer?
If the phasors are drawn to represent the maximum values instead of the rms values, what would happen to the phase angle between quantities?
|
76 videos|152 docs|62 tests
|