Get the App Signup / Login
Sign in Open App

Test: Polynomials (Easy)


15 Questions MCQ Test | Test: Polynomials (Easy)


Description
Attempt Test: Polynomials (Easy) | 15 questions in 15 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study for Class 10 Exam | Download free PDF with solutions
QUESTION: 1

Write down the degree of following polynomials in x: 3 - 2x

Solution: The exponent of the first term -2x = 1 Therefore, the degree of the polynomial 3 - 2x = 1

QUESTION: 2

Find the degree of the given algebraic expression ax2 + bx + c

Solution:

We know that the degree is the term with the greatest exponent.

 

 

QUESTION: 3

If x = 2 and x = 3 are zeroes of the quadratic polynomial x2 + ax + b, the values of a and b respectively are

Solution: If 2 and 3 are the zeroes of the quadratic polynomial then (x - 2)(x - 3) are the factors of the polynomial Thus,

QUESTION: 4

Write the degree of each of the following polynomials: 1 / 2y7 - 12y6 + 48y5 - 10
Solution: The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

QUESTION: 5

3x3 - 2x - x + 3 is an example of
Solution:

3x3 - 2x - x + 3 = 3x3 - 3x + 3 is an example of cubic polynomials. A cubic polynomial is a polynomial of degree 3. Since the highest degree is 3.

 

 

QUESTION: 6

Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most
Solution:

The polynomial ax2 + bx + c has three terms. The first one is ax2, the second is bx, and the third is c. The exponent of the first term is 2. The exponent of the second term is 1 because bx = bx1. The exponent of the third term is 0 because c = cx0. Since the highest exponent is 2, therefore, the degree of ax2 + bx + c is 2. Since, the degree of the polynomial is 2, hence, the polynomial ax2 + bx + c can have zero, one or two zeroes. Hence, the polynomial ax2 + bx + c can have at most two zeros.

QUESTION: 7

The zero of polynomial p(x) = 4x + 5 is:
Solution: Given, f(x) = 4x + 5.

To find the zero of a polynomial, we use f(x) = 0.

Then, 4x + 5 = 0 ⟹ 4x = −5 ⟹ x = -5 / 4

Hence, −5 / 4 ​ is the zero of the polynomial 4x + 5.

QUESTION: 8

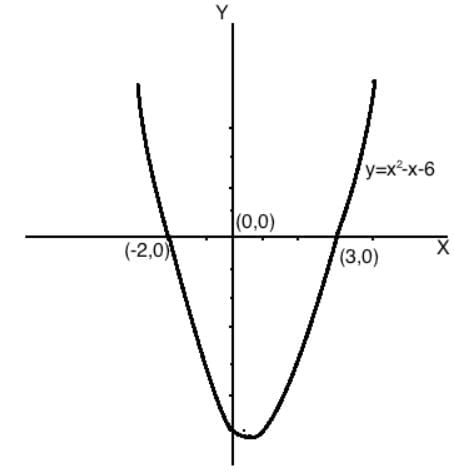
Draw the graphs of y = x2 - x - 6 and find the zeroes in each case.
Solution: Clearly graph of y = x2 − x − 6 cut the x-axis at x = −2, 3. ⇒ x = −2, 3 are zeroes of y = x2 − x − 6.

when x = −2; y = 4 + 2 − 6 = 0

when x = 3; y = 9 − 3 − 6 = 0

QUESTION: 9

Assertion: Degree of a zero polynomial is not defined.

Reason: Degree of a non-zero constant polynomial is 0
Solution: We know that, The constant polynomial 0 is called a zero polynomial. The degree of a zero polynomial is not defined, a Assertion is true. The degree of a non-zero constant polynomial is zero. A Reason is true. Since both Assertion and Reason are true and Reason is not a correct explanation of Assertion. The correct answer is B.

QUESTION: 10

Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively: 0, 3
Solution: Given: Sum of zeroes = α + β = 0 Product of zeroes = αβ = 3 Then, the quadratic polynomial = x2 - (sum of zeroes )x + product of zeroes = x2 - (0)x + 3 = x2 + 3

QUESTION: 11

Find the variable of the linear polynomial t + 5.
Solution: Since in a polynomial x + a, x is a variable and a is a constant term, therefore, the linear polynomial t + 5 has a variable t and 5 is a constant term.

QUESTION: 12

Find the zero of the polynomial in each of the following in the following case: p(x) = x +

5
Solution: Putting p(x) = 0 we get => x + 5 = 0 => x = - 5

∴ -5 is zero of the polynomial

QUESTION: 13

The variable in the quadratic polynomial t2 + 4t + 5 is
Solution: Since in a standard quadratic polynomial x + x + a, x is a variable and a is a constant term, therefore, in the given polynomial t2 + 4t + 5 we have variable t and 5 is a constant term.

QUESTION: 14

What must be subtracted from the polynomial 8x4 + 14x3 + x2 + 7x + (8 so that the resulting polynomial is exactly divisible by 4x2 - 3x + 2?
Solution:

Thus, when 6x + 2 is subtracted from the given polynomial 8x4 + 14x3 + x2 + 7x + 8, then it will be divisible by 4x2 - 3x + 2.

QUESTION: 15

Classify the following polynomial based on their degree: 3x2 + 2x + 1
Solution: A polynomial is a function of the form f(x) = anxn + an−1xn−1 +...+ a2x2 + a1x + a0 ​

where an, an−1,... a2, a1, a0. are constants and n is a natural number.

Let p(x) = 3x2 + 2x + 1

The degree of a polynomial is the highest power of x in its expression.

Constant (non-zero) polynomials, linear polynomials, quadratics, cubics and quartics are polynomials of degree 0, 1, 2 , 3 and 4 respectively.

Highest power of x in p(x) is = 2

Thus, the degree of p(x) is 2.

Hence, it is a quadratic polynomial.

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us