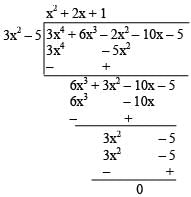Test: Polynomials (Hard) - Class 10 MCQ
20 Questions MCQ Test - Test: Polynomials (Hard)
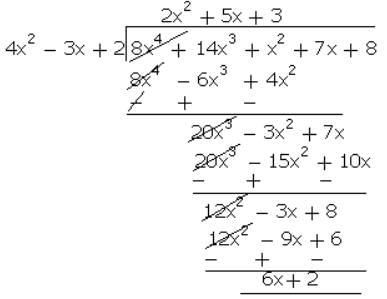
What must be subtracted from the polynomial 8x4 + 14x3 + x2 + 7x + (8 so that the resulting polynomial is exactly divisible by 4x2 - 3x + 2?
Find the smallest solution in positive integers of x2 - 14y2 = 1
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Obtain all other zeroes of 3x4 + 6x3 - 2x2 - 10x - 5, if two of its zeros are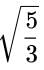 and
and 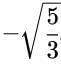 .
.
The zeroes of the quadratic polynomial 4x2 + 87x + 125 are
Zeroes of the quadratic polynomial x2 + 3x -(a + 2)(a - 1) is
If one zero of 3x - 8x + 2k + 1 is Severn times the other, then k is____.
The graph of a quadratic polynomial p(x) = 5x2 + 3x + 2 is an upward parabola.
The graph of a quadratic polynomial q(x) = - 3x2 + 2 is an upward parabola.
If two zeroes of the polynomial (x3 − 5x2 −16x + 80) are equal in magnitude but opposite in sign, then zeroes are
If p(x) is divided by g(x), then deg. p(x) = deg. g(x) - deg. q(x), where q(x) is the quotient.
A cubic polynomial must have a minimum of one and maximum of three zeroes.
If two of the zeroes of a cubic polynomial are zero, then it does not contain linear and constant terms.
If the zeroes of a quadratic polynomial ax2 + bx + c are both positive, then a, b and c all have the same sign.
x2 - 1 can be the quotient in the division of x6 − 2x3 + x − 1 by a polynomial of degree 5.
Let p(x) = ax2 + bx + c be a quadratic polynomial can have at most