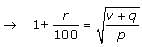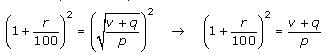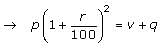Test: Population Growth - GMAT MCQ
8 Questions MCQ Test Quantitative for GMAT - Test: Population Growth
Jolene entered an 18-month investment contract that guarantees to pay 2 percent interest at the end of 6 months, another 3 percent interest at the end of 12 months, and 4 percent interest at the end of the 18 month contract. If each interest payment is reinvested in the contract, and Jolene invested $10,000 initially, what will be the total amount of interest paid during the 18-month contract?
Wes works at a science lab that conducts experiments on bacteria. The population of the bacteria multiplies at a constant rate, and his job is to notate the population of a certain group of bacteria each hour. At 1 p.m. on a certain day, he noted that the population was 2,000 and then he left the lab. He returned in time to take a reading at 4 p.m., by which point the population had grown to 250,000. Now he has to fill in the missing data for 2 p.m. and 3 p.m. What was the population at 3 p.m.?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
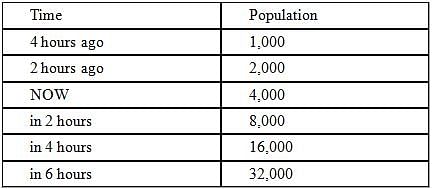
The population of locusts in a certain swarm doubles every two hours. If 4 hours ago there were 1,000
locusts in the swarm, in approximately how many hours will the swarm population exceed 250,000 locusts?
locusts in the swarm, in approximately how many hours will the swarm population exceed 250,000 locusts?
An investor purchased a share of non-dividend-paying stock for p dollars on Monday. For a certain number of days, the value of the share increased by r percent per day. After this period of constant increase, the value of the share decreased the next day by q dollars and the investor decided to sell the share at the end of that day for v dollars, which was the value of the share at that time. How many working days after the investor bought the share was the share sold, if
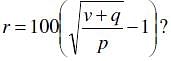
A certain investment grows at an annual interest rate of 8%, compounded quarterly. Which of the following equations can be solved to find the number of years, x, that it would take for the investment to increase by a factor of 16?
Jim needs $1,000 to buy a new flat-screen TV. Since he has only $7, he borrows the remanining balance from his sister Mary. The loan will be repaid in 3 annual installments at an interest rate of 10%, compounded annually. The formula for calculating the monthly payment P is P = (L x C x r) / (C – 1) where L = amount of the loan, r = annual interest rate, and C = compounding factor = (1 + r)N where N = number of annual payments. How much does Jim have to pay Mary at the end of each of the next 3 years (rounded to the nearest penny)?
Louie takes out a three-month loan of $1000. The lender charges him 10% interest per month compounded monthly. The terms of the loan state that Louie must repay the loan in three equal monthly payments. To the nearest dollar, how much does Louie have to pay each month?
Donald plans to invest x dollars in a savings account that pays interest at an annual rate of 8% compounded quarterly. Approximately what amount is the minimum that Donald will need to invest to earn over $100 in interest within 6 months?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|