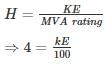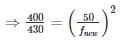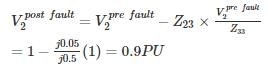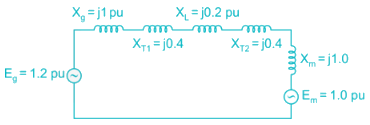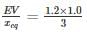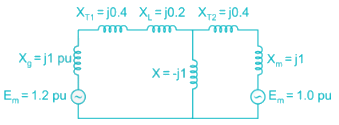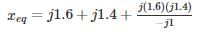Test: Power Systems- 8 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Power Systems- 8
The steady state stability limits for round rotor and salient pole 3 – phase synchronous generator are attained at the value of power angle δ
The inertial constant of 500 MVA, 13 kV generator is 8 MJ/MVA. The kinetic energy stored in the rotor at the synchronous speed is – (in MJ)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An alternator is connected to an infinite bus as shown in the figure. It delivers 1.0 p.u. current at 0.707 p.f lagging at V = 1.0 p.u. The reactance Xd of the alternator is 1.4 p.u. keeping the active power fixed, if the excitation reduced, the critical excitation corresponding to operation at stability limit is ______


A 50 Hz. 4 pole turbo generator rated 200 MVA, 13 kV has an inertia constant of 6 MJ/MVA. If mechanical input is suddenly raised to 100 MW for an electrical load of 80 MW, then its rotor accelerations – (in elec-deg/sec2)
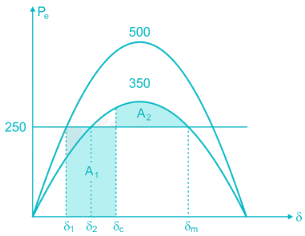
A synchronous generator is feeding 250 MW to a large 50 Hz network over a double circuit transmission line. The maximum steady state power that can be transmitted over the line with both circuits in operation is 500 MW and is 350 MW with any one of the circuits. A solid three phase fault occurring at the network end of one of the lines causes it to trip. Calculate the critical clearing angle in which the circuit breakers must trip so that synchronism is not lost.
A 50 Hz synchronous generator is connected to an infinite bus through a line. The pu. reactances of the generator and the lines are j 0.4 pu and j 0.2 pu respectively. The generator no-load voltage is 1.2 pu and that of the infinite bus is 1.0 pu. The inertia constant of the generator is 4 MW-Sec/MVA. Determine the frequency (in Hz) of natural oscillations if the generator is loaded to 70% of its maximum power transfer capacity and small perturbation is given
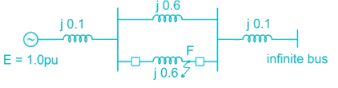
A generator is delivering 1.0 pu power shown in the figure. A three-phase fault occurs at point F. The critical clearing angle for clearing the fault with simultaneous opening of breaker 1 and 2 is
A 100 MVA generator operates on full load of 50 Hz frequency. The load is suddenly reduced to 60 MW. The system value begins to close only after 0.5 sec. and if the value of the inertia constant (H) is 4 MJ/MVA, then the frequency at 0.5 sec is – (in Hz)
In a power system has pre-fault voltage 1 PU and ZBUS given as
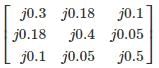
If 3ϕ fault occur at bus 3 find the post-fault voltage at bus 2 is ______ (in PU)
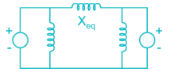
In the system shown in the figure, a static three-phase capacitor of reactance 1 pu per phase is connected through a switch at motor bus bar. The internal voltage and reactances are specified. The steady state power limits when the switch is open and closed respectively are



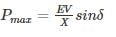
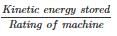
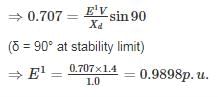
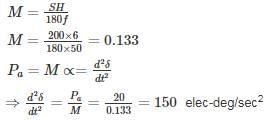
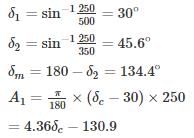
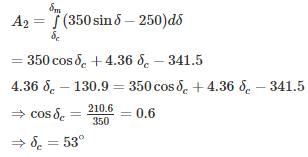
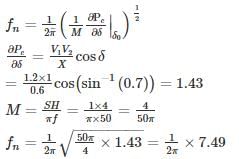 fn = 1.19 Hz.
fn = 1.19 Hz.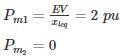
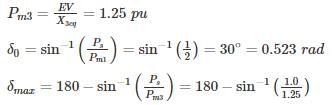 = 126.86° = 2.214 rad
= 126.86° = 2.214 rad