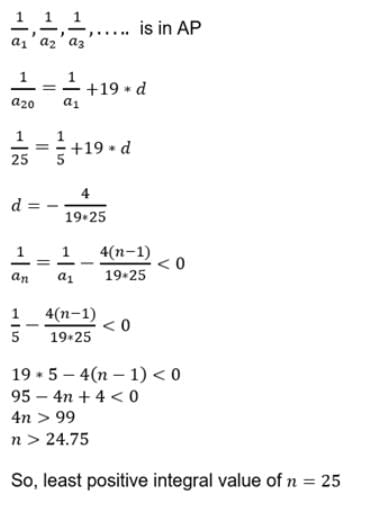Test: Previous Year Questions- Sequences & Series- 2 - JEE MCQ
18 Questions MCQ Test - Test: Previous Year Questions- Sequences & Series- 2
(a) Consider an infinite geometric series with first term a and common ratio r. If the sum is 4 and the second term is 3/4, then [JEE 2000, (scr.), 1 + 1]
(A) a = 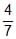 , r =
, r = 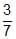 (B) a = 2, r =
(B) a = 2, r = 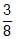 (C) a = , r =
(C) a = , r = 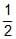 (D) a = 3, r =
(D) a = 3, r = 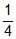
(b) If a, b, c, d are positive real numbers such that a + b + c + d = 2, then M = (a + b) (c + d) satisifes the relation :
(A) 0 £ M £ 1 (B) 1 £ M £ 2 (C) 2 £ M £ 3 (D) 3 £ M £ 4
(c) The fourth power of the common difference of an arithmetic progression with integer entries added to the product of any four consecutive terms of it. Prove that the resulting sum is the square of an integer. [JEE 2000, (Mains), 4]
Given that a, g are roots of the equation, Ax2_4x+1 =0 and b, d the roots of the equation, Bx2 _ 6x + 1 = 0, find values of A and B, such that a, b, g & d are in H.P. [REE 2000, 5]
The sum of roots of the equation ax2 + bx + c = 0 is equal to the sum of squares of their reciprocals. Find whether bc2, ca2 and ab2 in A.P., G.P. or H.P. ? [ree 2001, 3]
Solve the following equations for x and y log2x + log4x + log16x +..............
........... = y = 4log4 x [ree 2001, 5]
a) Le a, b be the roots of x2 _ x + p = 0 and g, d the roots of x2 _ 4x + q = 0. If a, b, g, d are in G.P., then the integral values of p and q respectively, are
(A) _2, _32 (B) _2, 3 (C) _6, 3 (D) _6. _ 32
(b) If the sum of the first 2n terms of the A.P. 2, 5, 8,... ..........is equal to the sum of the first n terms of the A.P. 57, 59, 61,......., then n equals
(A) 10 (B) 12 (C) 11 (D) 13
(c) Let the positive numbers a, b, c, d be in A.P. Then abc, abd, acd, bcd are [Jee 2001, (Scr.) 1 + 1 + 1]
(A) NOT in A.P./G.P./ H.P. (B) in A.P. (C) in G.P. (D) in H.P.
(d) Let a1, a2,..... be positive real numbers in G.P. For each n, let An, Gn, Hn be respectively, the arithmetic mean, geometric mean, and harmonic mean of a1, a2,..........., an. Find an expression for the G.M. of G1, G2,............, Gn in terms of A1, A2,...........,An, H1, H2,........,Hn. [JEE 2001 (Mains), 5]
(a) Suppose a, b, c are in A.P. and a2, b2, c2 are in G.P. if a < b < c and a + b + c = 3/2, then the value of a is [JEE 2002 (Scr.), 3]
(A) (B)
(C)
(D)
(b) Let a, b be positive real numbers. If a, A1, A2,b are in A.P. ; a, G1, G2, b are in G.P. and a, H1, H2, b are in H.P. show that=
=
. [JEE 2002 (Mains), 5]
The first term of an infinite geometric progression is x and its sum is 5. Then [JEE 2004 (Scr.)]
(a) In the quadratic equation ax2 + bx + c = 0, If D = b2 _ 4ac and a + b, a2 + b2, a3+ b3, are in G.P. where a, b are the roots of ax2 + bx + c = 0, then [JEE 2005 (Scr.)]
(A) D ¹ 0 (B) bD = 0 (C) cD = 0 (D) D = 0
(b) If total number of runs scored in n matches is (2n+1 _ n _ 2) where n > 1, and the runs scored in the kth match are given by k.2n+1_k, where 1 £ k £ n. Find n. [JEE 2005 (Mains), 2]
If An = _
+ ............(_1)n _ 1
and Bn = 1 _ An, then find the minimum natural number n0 such that Bn > An n > n0. [JEE 2006, 6]
Let Vr denote the sum of first r terms of an arithmetic progression (A.P.) whose first term is r and the common difference is (2r _ 1). Let Tr = V r + 1 _ Vr _ 2 and Qr= Tr + 1 _ Tr for r = 1, 2,.....
(a) The sum V1 + V2 + ....... + Vn is
(A) n(n+1)(3n2 _n+1) (B)
n(n+1)(3n2+n+2) (C)
n (2n2_n+1) (D)
(2n3_2n+3)
(b) Tr is always
(A) an odd number (B) an even number (C) a prime number (D) a composite number
(c) Which one of the following is a correct statement ?
(A) Q1, Q2, Q3,.... are in A.P., with common difference 5
(B) Q1, Q2, Q3,.... are in A.P., with common difference 6
(C) Q1, Q2, Q3,.... are in A.P., with common difference 11
(D) Q1 = Q2 = Q3 =.... [JEE 2007, 4 + 4 + 4]
Let A1, G1, H1 denote the arithmetic, geometric and harmonic means, respectively, of two distinct positive numbers. For n ³ 2, Let An _ 1 and Hn _ 1 have arithmetic, geometric and harmonic means as An, Gn, Hn respectively
(a) Which one of the following statements is correct ?
(A) G1 > G2 > G3 > ........ (B) G1 < G2 < G3 < ........
(C) G1 = G2 = G3 = ........ (D) G1 < G3 < G5 < ...... and G2 > G4 > G6 > ......
(b) Which one of the following statement is correct ?
(A) A1 > A2 > A3 > ........ (B) A1 < A2 < A3 < ........
(C) A1 > A3 > A5 > .....and A2 < A4 < A6 < ........ (D) A1 < A3 < A5 < .....and A2 > A4 > A6 > ........
(c) Which one of the following statement is correct ? [JEE 2007, 4 + 4 + 4]
(A) H1 > H2 > H3 > ........ (B) H1 < H2 < H3 < ........
(C) H1 > H3 > H5 > .....and H2 < H4 < H6 < ........ (D) H1 < H3 < H5 < .....and H2 > H4 > H6 > ........
(a) A straight line through the vertex P of a triangle PQR intersects the side QR at the point S and the circumcircle of the triangle PQR at the point T. If S is not the centre of the circumcircle, then [JEE 2008, 4]
(A) (B)
(C)
(D)
(b) Supose four distinct positive numbers a1, a2, a3, a4 are in G.P. Let b1 = a1, b2 = b1 + a2, b3 = b2 + a3 and b4 = b3 + a4. [JEE 2008, 3]
Statement_1 : The numbers b1, b2, b3, b4 are neither in A.P. nor in G.P.
Statement_2 : The numbers b1, b2, b3, b4 are in H.P.
(A) Statement (1) is true and statement (2) is true and statement (2) is correct explanation for (1)
(B) Statement (1) is true and statement (2) is true and statement (2) is NOT correct explanation for (1)
(C) Statement (1) is true but (2) is false
(D) Statement (1) is false but (2) is true
If the sum of first n terms of an A.P. is cn2, then the sum of squares of these n terms is [JEE 2009, 3]
Let Sk, K = 1, 2, ...., 100 denote the sum of the infinite geometric series whose first term is and the common ratio is 1/k. Then the value of
is [JEE 2010]
Let a1, a2, a3, ....., a11 be real numbers satisfying
a1 = 15, 27 _ 2a2 > 0 and ak = 2ak-1 _ ak-2 for k = 3, 4, ...., 11
If , then the value of
is equal to [JEE 2010]
The minimum value of the sum of real numbers a_5, a_4, 3a_3, 1, a8 and a10 with a > 0 is [JEE 2011]
Let a1, a2, a3, ..., a100 be an arithmetic progression with a1 = 3 and Sp = , 1 £ p £ 100. For any integer n with 1 £ n £ 20. let m=5n. If
does not depend on n, then a2 is [JEE 2011]
Let a1, a2, a3, ..... be in harmonic progression with a1 = 5 and a20 = 25. The least positive integer n for which an < 0 is [JEE 2012]