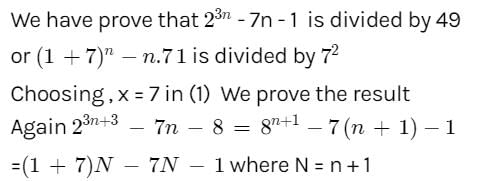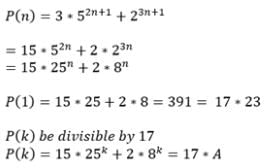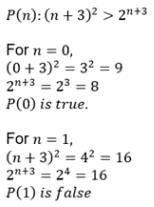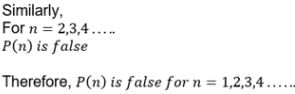Test: Principle Of Mathematical Induction- 2 - Commerce MCQ

If n is a +ve integer, then 7²ⁿ−4 is divisible by

Let P (k) = 1 + 3 + 5 + …………….+ (2k – 1) = (3+k²).Then which of the following is true ?

The inequality 2ⁿ<n!,n∈N is true for :

For each n ∈ N,a²ⁿ⁻¹+b²ⁿ⁻¹ is divisible by :

For each n ∈ N, n (n + 1) (2n + 1) is divisible by :

For each n ∈ N, 3(5²ⁿ⁺¹)+2³ⁿ⁺¹ is divisible by :

For each n ∈ N, 2³ⁿ−1 is divisible by :

For each n ∈ N, 3²ⁿ−1 is divisible by :

The statement P (n) : “(n+3)² > 2ⁿ⁺³ “ is true for :

The smallest positive integer ‘n‘ for which 2ⁿ(1×2×3×...............×n) < nⁿ holds is :

If 10ⁿ+3×4ⁿ⁺¹+k is divisible by 9 for all n ∈ N, then the least positive integral value of k is 

The smallest positive integer n, for which ( 1 × 2 × 3 ×……×n ) 

Let P(n) : n²−n+41 is a prime number . then :

Let that P(n) ⇒ P(n+1) for all natural numbers n. also, if P (m) is true, m ∈ N, then we conclude that

Consider the statement P (n) : “n² ≥ 100 “. Here P(n) ⇒ P(n+1) for all natural numbers n. Does it mean

The smallest positive integer ‘n‘ for which P (n) : 2ⁿ < (1×2×3×............×n) holds is :

If xⁿ−1 is divisible by x – k for all n belongs to natural numbers N, then the least positive integral value of k is :

A student was asked to prove a statement P (n) by method of induction. He proved P (k + 1) is true whenever P (k) Is true for all k ≥ 5 , k ∈ N and P (5) is true. On the basis of this he could conclude that P (n) is true

If a,b,c ∈ N, aⁿ+bⁿ is divisible by c, when n is odd but not when n is even, then the value of c is :

1.2.3 + 2.3.4 + 3.4.5 + ………..up to n terms is equal to :

The number of terms in the expansion of (x+y+z)ⁿ is

The sum of the terms in the nth bracket of the series 1 + (2+3+4) + (5+6+7+8+9) ….is