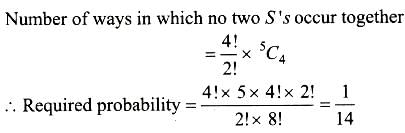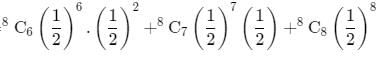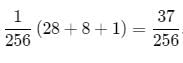Test: Probability- 1 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Probability- 1
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is
Two players toss four coins each. The probability that both obtain the same number of heads is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If three dice are thrown, then the probability that they show the numbers in A.P. is
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is
A coin is tossed once. If a head comes up, then it is tossed again and if a tail comes up, a dice is thrown. The number of points in the sample space of experiment is
A drawer contains 5 black socks and 4 blue socks well mixed. A person searches the drawer and pulls out 2 socks at random. The probability that they match is
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is
A and B take turn in throwing a pair of dice. A wins if he throws a total of 5 before B throws a total of 7. If A has the first throw, the probability of his winning the game is
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is
If the letters of the word ‘ INDEPENDENCE ‘ are written down at random in a row, then the chance that no two E’s occur together is
The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is
A person throws successively with a pair of dice. The chance that he throws 9 before he throws 7 is
Let A be set of 4 elements. From the set of all functions from A to A, a function is chosen at random. The chance that the selected function is an onto function is
Both A and B throw a dice. The chance that B throws a number higher than that thrown by A is
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is
Two dice are thrown. The number of sample points in the sample space when 6 does not appear on either dice is
8 coins are tossed at a time. The probability of getting 6 heads up is
A dice is rolled 6 times. The probability of obtaining 2 and 4 exactly three times each is
A dice has 3 faces each bearing ‘ 2 ‘ and three faces each bearing ‘ 6 ‘. It is rolled once. The probability of showing up ‘a six ‘ is
Neelam and Nidhi throw with a dice. The chance that both Neelam and Nidhi throw the same number is
A dice is tossed once and even number has come up. The chance that it is either 2 or 4 is
What is the probability of getting a sum of eight if two dice are thrown at once?
The probability of having atleast one head in 5 throws of a coin is
A fair coin is tossed a fixed number of times. If the probability of getting 4 heads is equal to the probability of getting 7 heads, then the probability of getting 2 heads is
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|