Test: Probability And Expected Value By Mathematical Expectation- 8 - CA Foundation MCQ
30 Questions MCQ Test - Test: Probability And Expected Value By Mathematical Expectation- 8
A dice is thrown once. What is the mathematical expectation of the number on the dice?
A bag contains 5 Red balls, 4 Blue Balls and 'm' Green Balls. If the random probability of picking two green balls is 1/7. What is the no. of green Balls (m).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider two events A and B not mutually exclusive, such that P(A) = 1/4, P(B) =2/5, P(A∪B) = 1/2, then P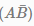 
is
isThe probability of Girl getting scholarship is 0.6 and the same probability for Boy is 0.8. Find the probability that at least one of the categories getiing scholarship.
In a pack of playing cards with two jokers probability of getting king of spade is
The odds in favour of A solving a problem is 5:7 and Odds against B solving the same problem is 9:6. What is the probability that if both of them try, the problem will be solved?
If x be the sum of two numbers obtained when two die are thrown simultaneously then P(x ≥ 7) is
E(13x+9)=___________.
The probability of winning of a person is 6/11 and at a result he gets Rs.77/-. The expectation of this person is
E(XY) is also known as:
If P(A/B) = P
If P(A∪B) = P(A), Find P(A∩B).
Consider Urn I :2 white balls, 3 black balls
Urn II : white balls, 6 black balls
One ball is randomly transferred from first to second Urn, then one ball is drawn from II Urn. The probability that drawn ball is white is
A bag contains 3 white and 5 black balls and second bag contains 4 white and 2 black balls. If one balls is taken from each bag, the probability that both the balls are white is___________
If A and B are two independent events and P(AUB) =2/5; P(B) = 1/3. Find P(A).
In a throw of dice what is the probability of getting number greater than 5
If 10 men, among whom are A and B, stand in a row, what is the probability that there will be exactly 3 men between A and B?
The probability of an event can assume any value between:
If P(A∩B) = P(A) x P(B), then the events are:
A random variable X has the following probability distribution:
Find E (X2) and E(2X+5).
A bag contains 12 balls of which 3 are red 5 balls are drawn at random. Find the probability that in 5 balls 3 are red.
The probability that a trainee will remain with a company is 0.8. The probability that an employee earns more than Rs. 20,000 per month is 0.4. The probability that an employee, who was a trainee and remained with the company or who earns more than Rs. 20,000 per month is 0.9. What is the probability that an employee earns more than Rs. 20.000 per month given that he is a trainee, who stayed with the company?
Daily demand for calculators is having the following probability distribution:
Determine the variance of the demand:
P(A) = 2/3; P(B) = 3/5; P(A∪ B) = 5/6. Find P (B/A)
The odds are 9:5 against a person who is 50 years living till he is 70 and 8:6 against a person who is 60 living till he is 80. Find the probability that at least one of them will be alive after 20 years:
An urn contains 6 white and 4 black balls. 3 balls are drawn without replacement. What is the expected number of black balls that will be obtained?
A random variable X has the following probability distribution
Then, P(x<3) would be:
The limiting relative frequency of probability is:
then find E(2x+5)
The theory of compound probability states that for any two events A and B:
Top Courses for CA Foundation
Important Questions for Probability And Expected Value By Mathematical Expectation- 8
Probability And Expected Value By Mathematical Expectation- 8 MCQs with Answers
Online Tests for Probability And Expected Value By Mathematical Expectation- 8
|
© EduRev
|
Education Revolution
|
|
